Giá trị lớn nhất của hàm số
y
=
-
x
2
+
4
x
trên khoảng
0
;
3
là: ...
Đọc tiếp
Giá trị lớn nhất của hàm số y = - x 2 + 4 x trên khoảng 0 ; 3 là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
9 tháng 10 2019
Đúng(0)
Những câu hỏi liên quan
CM
30 tháng 6 2017
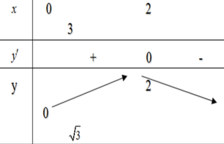
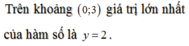
Chọn C
Tập xác định của hàm số là ℝ .
Ta có: 
Vì trên khoảng - 4 3 ; 0 hàm số đạt giá trị lớn nhất tại x = -1 nên hàm số đạt cực trị tại x = -1( cũng là điểm cực đại của hàm số) và a > 0.
Khi đó f'(x) = 0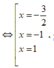 
( đều là các nghiệm đơn)
Hàm số đạt cực đại tại x = -1 nên có bảng biến thiên:
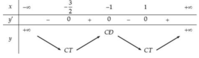
=> x = - 3 2 là điểm cực tiểu duy nhất thuộc - 2 ; - 5 4
Vậy hàm số đạt giá trị nhỏ nhất tại x = - 3 2 trên đoạn - 2 ; - 5 4
13 tháng 2 2023
a: Tọa độ đỉnh là:
\(\left\{{}\begin{matrix}x=\dfrac{-10}{2\cdot\left(-3\right)}=\dfrac{10}{6}=\dfrac{5}{3}\\y=-\dfrac{10^2-4\cdot\left(-3\right)\cdot\left(-4\right)}{4\cdot\left(-3\right)}=\dfrac{13}{3}\end{matrix}\right.\)
Bảng biến thiên:
| x | -\(\infty\) 5/3 +\(\infty\) |
| y | +\(\infty\) 13/3 -\(\infty\) |
b: Hàm số đồng biến khi x<5/3; nghịch biến khi x>5/3
Giá trị nhỏ nhất là y=13/3 khi x=5/3
CM
7 tháng 1 2017
Đáp án C
Ta có: y = x + 1 x 2 + 1 ⇒ y 2 x 2 + 1 = x + 1 2
⇔ x 2 y 2 − 1 − 2 x + y 2 − 1 = 0 1
Ta có: Δ ' 1 = 1 − y 2 − 1 2 ≥ 0 ⇔ − 1 ≤ y 2 − 1 ≤ 1
⇒ y 2 ≤ 2 ⇒ y ≤ 2 ⇒ max y = 2
PT
1
CM
19 tháng 9 2019
Đáp án C
Xét trên 0 , π ta có y ' = 1 - 2 sin x ⇒ y ' = 0 ⇔ sin x = 1 2 ⇔ x = π 4 ta có BBT như sau
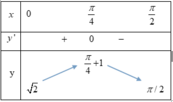
Như vậy GTLN của hàm số là π 4 + 1