Xét hàm số f ( x ) = x 2 + ax + b . Gọi M là giá trị lớn nhất của hàm số trên [-1;3]. Giá trị của biểu thức a + 2b khi M nhỏ nhất là
A. 4
B. -4
C. 2
D. 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Xét hàm số f(x) = | x 2 + a x + b |. Theo đề bài, M là giá trị lớn nhất của hàm số trên [-1;3]
Suy ra
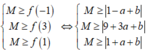
![]()
![]()
![]()
Nếu M = 2 thì điều kiện cần là ![]() và
và ![]() cùng dấu
cùng dấu
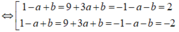
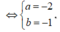
Ngược lại, khi 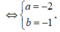
Ta có, hàm số ![]()
![]()
M là giá trị lớn nhất của hàm số f(x) trên [-1;3] ![]()
Vậy 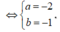
Ta có: a + 2b = -4.

Chọn C
Ta có ![]() . Dấu
. Dấu ![]() xảy ra khi
xảy ra khi ![]() .
.
Ta có ![]() . Dấu
. Dấu ![]() xảy ra khi
xảy ra khi ![]() .
.
Xét hàm số ![]() , có
, có ![]() .
.
Trường hợp 1: ![]()
![]() . Khi đó
. Khi đó ![]() .
.
Áp dụng bất đẳng thức ![]() ta có
ta có ![]() .
.
Trường hợp 2:![]()
![]() . Khi đó
. Khi đó 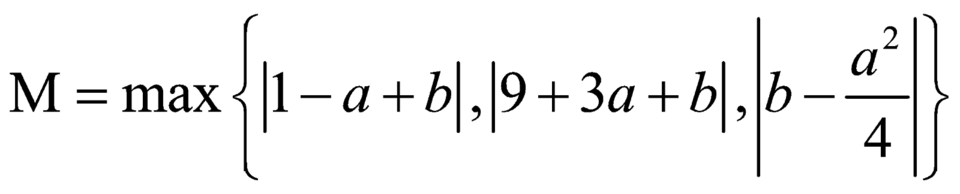 .
.
Áp dụng bất đẳng thức ![]() và
và![]() ta có
ta có 
![]()
![]() .
.
Suy ra ![]() .
.
Vậy ![]() nhận giá trị nhỏ nhất có thể được là
nhận giá trị nhỏ nhất có thể được là ![]() khi
khi 
![]() .
.
Do đó ![]() .
.

Ta có
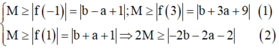
Từ (1) và (2), kết hợp với x + y + z ≥ x + y + z ta được
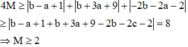
Giá trị nhỏ nhất của M là 2 .
Dấu bằng xảy ra khi
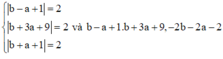
cùng dấu
Do đó a = - 2 b = - 1 ⇒ a b = 2
Chọn A.

Dựa vào bảng xét dấu của f '(x) ta có bảng biến thiên của hàm số trên đoạn [0;5] như sau
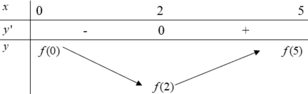
Suy ra ![]() Và
Và ![]()
Ta có ![]()
![]()
Vì f(x) đồng biến trên đoạn [2;5] nên ![]()
⇒ f(5)>f(0)
Vậy
![]()
Chọn đáp án D.
Chọn B
Ta có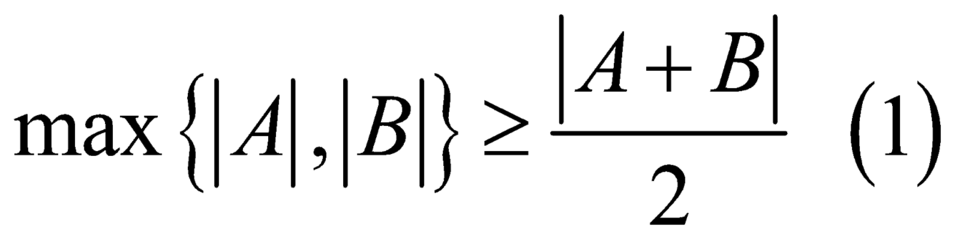 .
.
Dấu = xảy ra khi A=B.
Ta có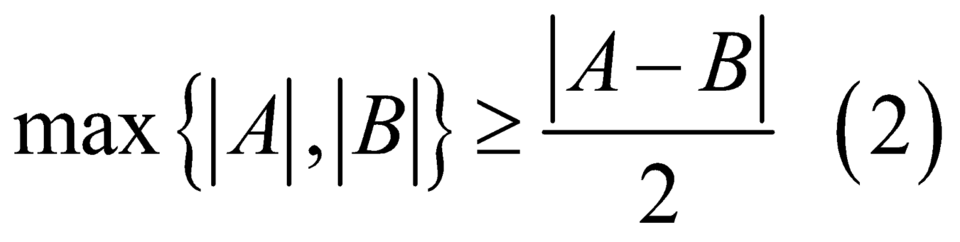 .
.
Dấu = xảy ra khi A= -B.
Xét hàm số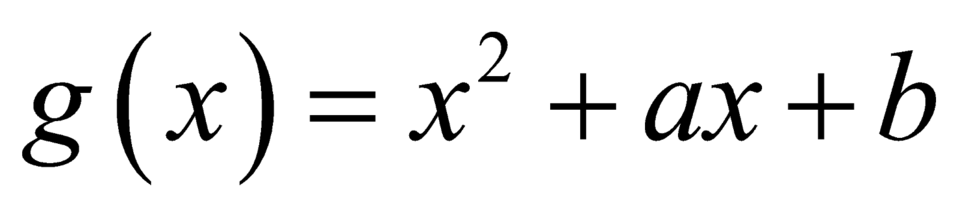 , có
, có 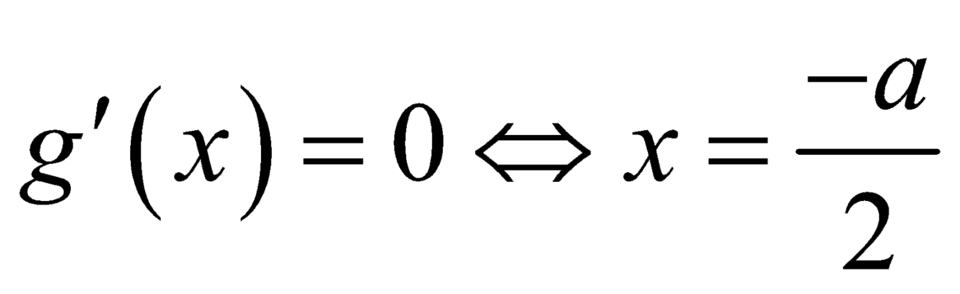 .
.
Trường hợp 1: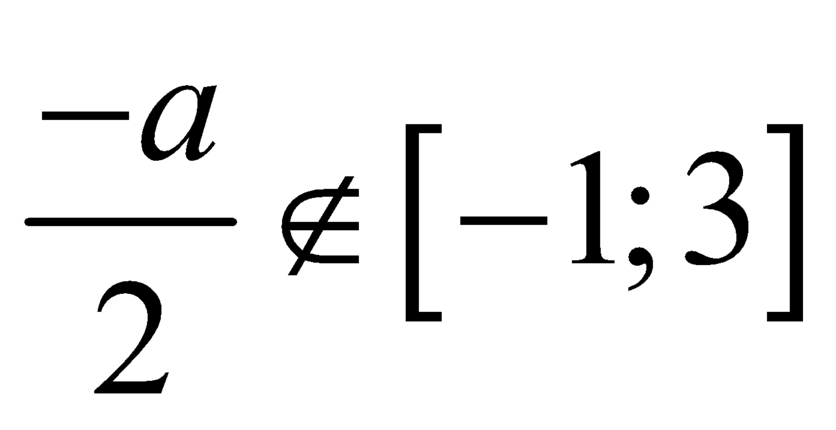
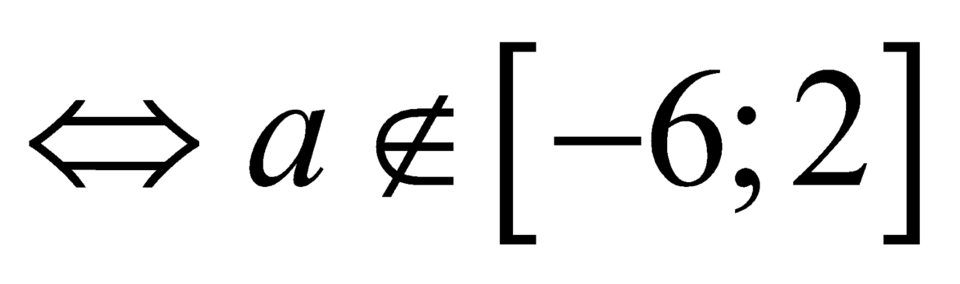 .
.
Khi đó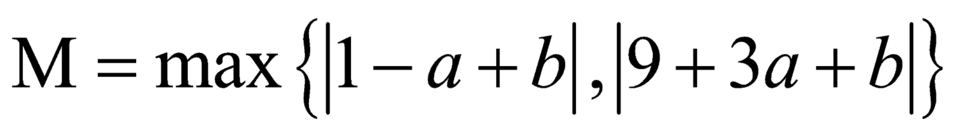 .
.
Áp dụng bất đẳng thức (1) ta có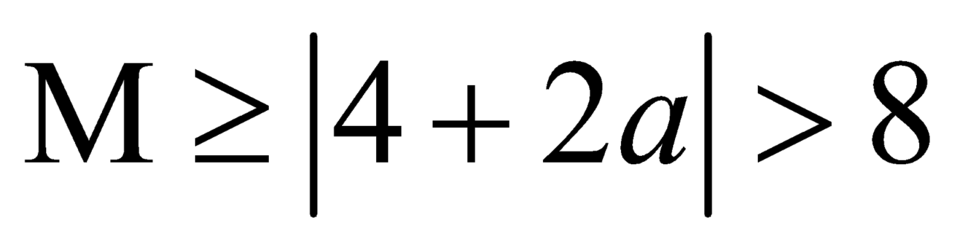 .
.
Trường hợp 2: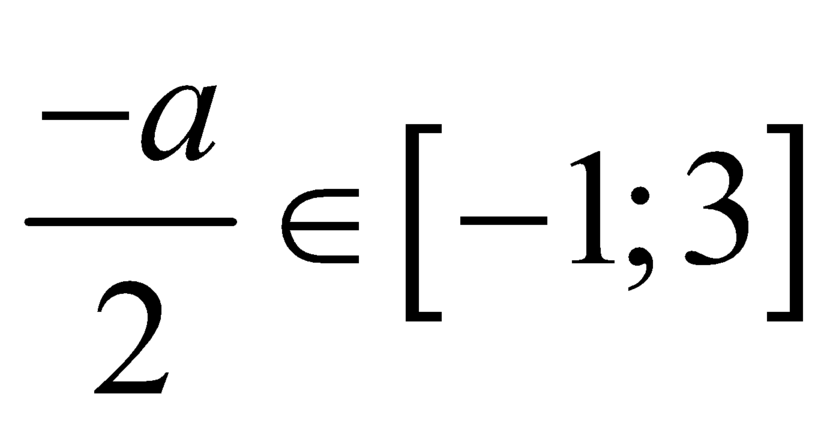
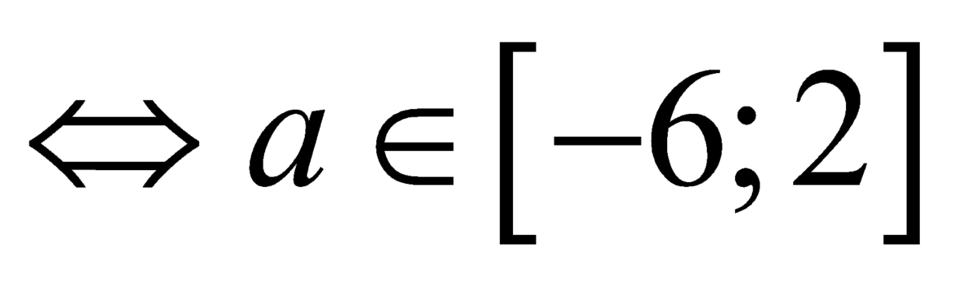 .
.
Khi đó .
.
Áp dụng bất đẳng thức (1) và(2) ta có
Suy ra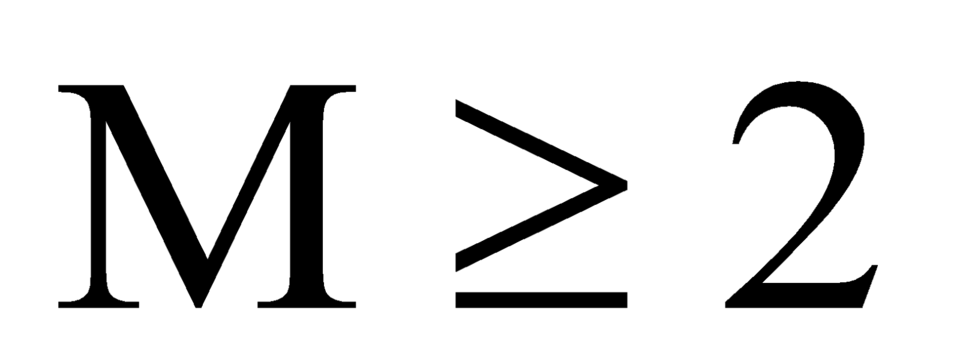 .
.
Vậy M nhận giá trị nhỏ nhất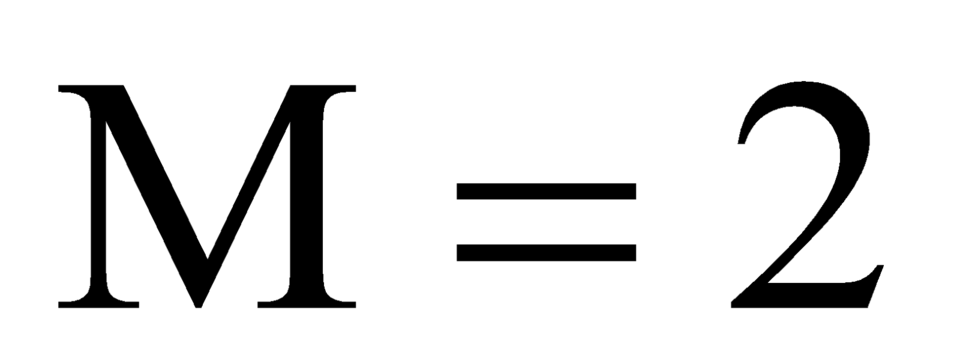 khi
khi
Do đó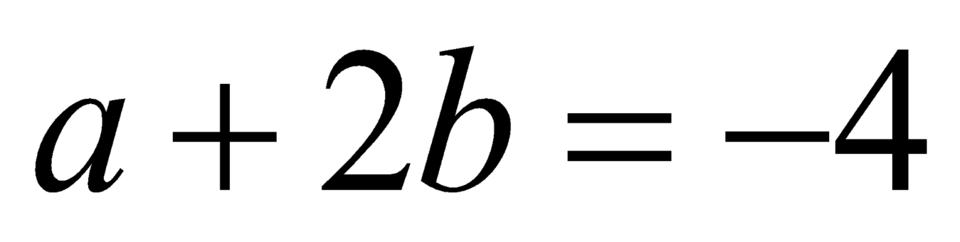 .
.