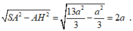Cho hình chóp S.ABC có đáy ABC là một tam giác vuông tại A, BC = 2a, A B C ^ = 60 0 . Gọi M là trung điểm của BC. Biết SA = SM = SB = a 39 3 Khoảng cách từ S đến mặt phẳng (ABC)
A. 2a
B. 4a
C. 3a
D. a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
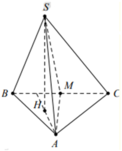
Tam giác ABM có A M = B M A B C ⏜ = 60 ° ⇒ Δ A B M đều cạnh a
Gọi H là tâm đường tròn ngoại tiếp Δ A B M
Mà S A = S B = S M ⇒ H là hình chiếu của S trên m p A B M
Tam giác SAH vuông tại H, có A H = a 3 3 ; S A = a 39 3
Suy ra S H = S A 2 − A H 2 = a 39 3 2 − a 3 3 2 = 2 a
Vậy d S ; ( A B C = S H = 2 a

Đáp án C
Ta có M là trung điểm của BC nên
Suy ra tam giác ABM là tam giác đều. Gọi H là hình chiếu vuông góc của S xuốn (ABM).
Suy ra H là tâm đường tròn ngoại tiếp tam giác ABM
![]()
Khi đó ![]()
![]()
Đáp án A
∆ AMB là tam giác đều cạnh a (vì AM = MB = a và A B M ^ = 60 0 )
Gọi H là chân đường cao hạ từ S xuống (ABC). Do SA = SB = SM nên H trùng với trọng tâm tam giác AMB.
Ta có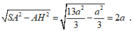
Vậy SH =