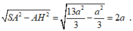Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta có M là trung điểm của BC nên
Suy ra tam giác ABM là tam giác đều. Gọi H là hình chiếu vuông góc của S xuốn (ABM).
Suy ra H là tâm đường tròn ngoại tiếp tam giác ABM
![]()
Khi đó ![]()
![]()

Kẻ MK vuông góc AC
\(\left\{{}\begin{matrix}MK\perp AC\subset\left(SAC\right)\\MK\perp SA\subset\left(SAC\right)\end{matrix}\right.\Rightarrow MK\perp\left(SAC\right)\)
\(\Rightarrow d\left(M,\left(SAC\right)\right)=KM=\dfrac{1}{2}AB=\dfrac{1}{2}\sqrt{16a^2-4a^2}=a\sqrt{3}\)

Chọn A

Gọi H là trung điểm của AC. Đỉnh S cách đều các điểm A, B, C
=> SH ⊥ (ABC)
Xác đinh được
![]()
Ta có MH // SA
![]()
Gọi I là trung điểm của AB => HI ⊥ AB
![]()
và chứng minh được HK ⊥ (SAB)
![]()
Trong tam giác vuông SHI tính được
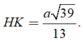

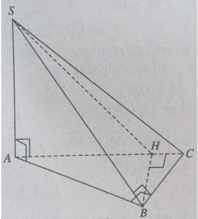
a) BC ⊥ SA & BC ⊥ AB) ⇒ BC ⊥ (SAB)
⇒ BC ⊥ SB.
⇒ tam giác SBC vuông tại B.
b) BH ⊥ AC & BH ⊥ SA ⇒ BC ⊥ (SAC)
⇒ (SBH) ⊥ (SAC).
c) d[B, (SAC)] = BH. Ta có:
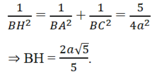

Đáp án A
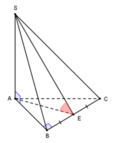
Do SA ⊥ (ABC) tại A nên A là hình chiếu của S lênmặt phẳng (ABC) kéo theo AE là hình chiếu của AE lên mặt phẳng (ABC).
![]()
Áp dụng định lý Py-ta-go trong ∆ S A E vuông tại B, ta có:
![]()
![]()
Trong ∆ S A E vuông tại A SA ⊥ (ABC) nên SA ⊥ AE, ta có:
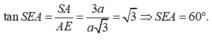
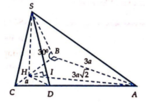
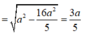
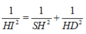
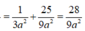
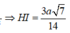

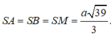 Khoảng cách từ điểm S đến mặt phẳng (ABC) là
Khoảng cách từ điểm S đến mặt phẳng (ABC) là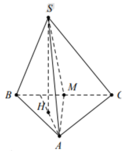

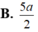
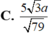
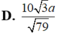
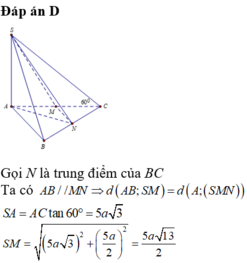
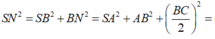
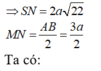
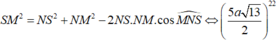
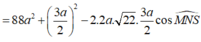
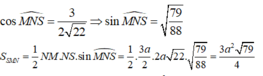

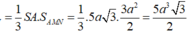
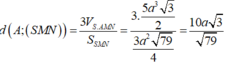
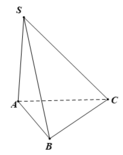
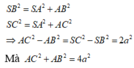
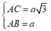
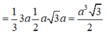
Đáp án A
∆ AMB là tam giác đều cạnh a (vì AM = MB = a và A B M ^ = 60 0 )
Gọi H là chân đường cao hạ từ S xuống (ABC). Do SA = SB = SM nên H trùng với trọng tâm tam giác AMB.
Ta có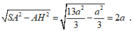
Vậy SH =