Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

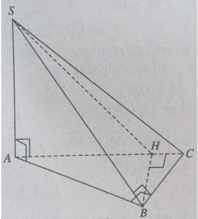
a) BC ⊥ SA & BC ⊥ AB) ⇒ BC ⊥ (SAB)
⇒ BC ⊥ SB.
⇒ tam giác SBC vuông tại B.
b) BH ⊥ AC & BH ⊥ SA ⇒ BC ⊥ (SAC)
⇒ (SBH) ⊥ (SAC).
c) d[B, (SAC)] = BH. Ta có:
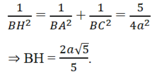

Đáp án A
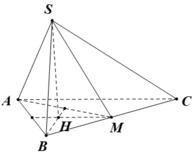
∆ AMB là tam giác đều cạnh a (vì AM = MB = a và A B M ^ = 60 0 )
Gọi H là chân đường cao hạ từ S xuống (ABC). Do SA = SB = SM nên H trùng với trọng tâm tam giác AMB.
Ta có 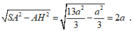
Vậy SH = 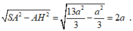

Đáp án C
Ta có M là trung điểm của BC nên
Suy ra tam giác ABM là tam giác đều. Gọi H là hình chiếu vuông góc của S xuốn (ABM).
Suy ra H là tâm đường tròn ngoại tiếp tam giác ABM
![]()
Khi đó ![]()
![]()


Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
là trọng tâm tam giác SAE.
Tứ diện AEND vuông tại đỉnh A nên
Vậy

Nhận xét
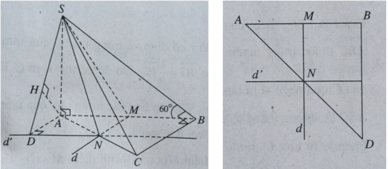
Gọi (α) là mặt phẳng qua SM và song song với AB.
Ta có BC // (α) và (ABC) là mặt phẳng chứa BC nên (ABC) sẽ cắt (α) theo giao tuyến d đi qua M và song song với BC, d cắt AC tại N.
Ta có (α) chính là mặt phẳng (SMN). Vì M là trung điểm AB nên N là trung điểm AC.
+ Xác định khoảng cách.
Qua N kẻ đường thẳng d’ song song với AB.
Gọi (P) là mặt phẳng đi qua SN và d’.
Ta có: AB // (P).
Khi đó: d(AB, SN) = d(A, (P)).
Dựng AD ⊥ d’, ta có AB // (SDN). Kẻ AH vuông góc với SD, ta có AH ⊥ (SDN) nên:
d(AB, SN) = d(A, (SND)) = AH.
Trong tam giác SAD, ta có 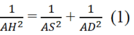
Trong tam giác SAB, ta có S A = A B . tan 60 o = 2 a 3 và AD = MN = BC/2 = a.
Thế vào (1), ta được
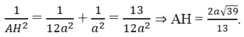

Gọi K là trung điểm của SA
=>KM//SC
=>SC//(KMB)
d(SC;BM)=d(S;(KBM))=SK/SA*d(A;(KBM))=d(A;(KBM))
=>ΔABC đều
=>BM vuông góc AC
=>BM vuông góc (SAC)
Kẻ AQ vuông góc KM
=>AQ vuông góc (KMB)
=>d(A;(KMB))=AQ
\(SC=\sqrt{9a^2+4a^2}=a\sqrt{13}\)
KM=1/2SC=a*căn 3/2
=>\(AQ=\dfrac{3\sqrt{13}}{13}\)
=>d(BM;SC)=3*căn 13/13

Đáp án A
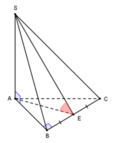
Do SA ⊥ (ABC) tại A nên A là hình chiếu của S lênmặt phẳng (ABC) kéo theo AE là hình chiếu của AE lên mặt phẳng (ABC).
![]()
Áp dụng định lý Py-ta-go trong ∆ S A E vuông tại B, ta có:
![]()
![]()
Trong ∆ S A E vuông tại A SA ⊥ (ABC) nên SA ⊥ AE, ta có:
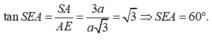
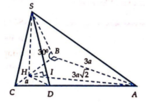
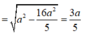
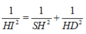
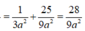
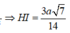

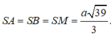 Khoảng cách từ điểm S đến mặt phẳng (ABC) là
Khoảng cách từ điểm S đến mặt phẳng (ABC) là

Kẻ MK vuông góc AC
\(\left\{{}\begin{matrix}MK\perp AC\subset\left(SAC\right)\\MK\perp SA\subset\left(SAC\right)\end{matrix}\right.\Rightarrow MK\perp\left(SAC\right)\)
\(\Rightarrow d\left(M,\left(SAC\right)\right)=KM=\dfrac{1}{2}AB=\dfrac{1}{2}\sqrt{16a^2-4a^2}=a\sqrt{3}\)