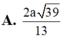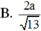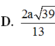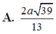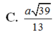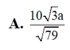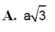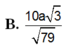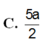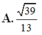Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

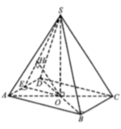
Đáp án: A.
§ Hướng dẫn giải:
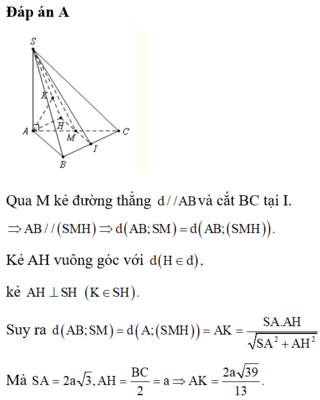
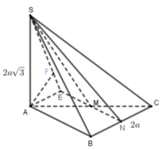
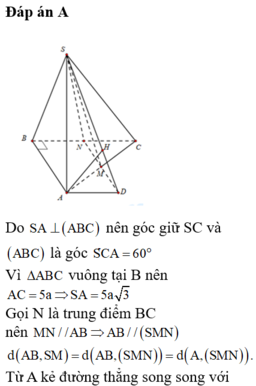
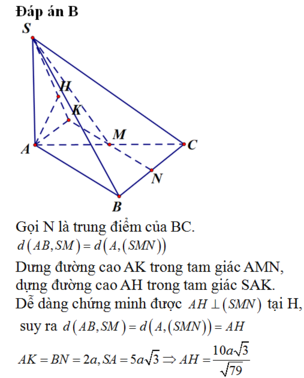
Gọi N là trung điểm của cạnh đáy AC.
Khi đó BC // (SMN)
⇒ d(SM,BC)=d(B,(SMN))=d(A,(SMN))
Gọi H là hình chiếu vuông góc của A trên đoạn SM.
Ta có thể chứng minh được M N ⊥ ( S A M )
từ đó A H ⊥ ( S M N )
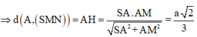

Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với (ABC) \(\Rightarrow SA\perp\left(ABC\right)\)
\(AB\perp BC\Rightarrow SB\perp BC\Rightarrow\widehat{SBA}\) là góc giữa 2 mặt phẳng (SBC) và mặt phẳng (ABC)
\(\Rightarrow\widehat{SBA}=60^o\)
\(\Rightarrow SA=AB.\tan\widehat{SBA}=2a\sqrt{3}\)
Mặt phẳng qua SM và song song với BC, cắt AC tại N
\(\Rightarrow MN||BC\) và N là trung điểm của \(AC\\ \)
\(MN=\frac{BC}{2}=a;BM=\frac{AB}{2}=a\)
Diện tích \(S_{BCNM}=\frac{\left(BC+MN\right).BM}{2}=\frac{3a^2}{2}\)
Thể tích \(V_{S.BCNM}=\frac{1}{3}S_{BCNM}.SA=a^3\sqrt{3}\)
Kẻ đường thẳng \(\Delta\) đi qua N, song song với AB
Hạ \(AD\perp\Delta\left(D\in\Delta\right)\Rightarrow AB||\left(SND\right)\)
\(\Rightarrow d\left(AB;SN\right)=d\left(AB,\left(SND\right)\right)=d\left(A,\left(SND\right)\right)\)
Hạ \(AH\perp SD\left(H\in SD\right)\Rightarrow AH\perp\left(SND\right)\Rightarrow d\left(A,\left(SND\right)\right)=AH\)
Tam giác SAD vuông tại A : \(\begin{cases}AH\perp SD\\AD=MN=a\end{cases}\)
\(\Rightarrow d\left(AB,SN\right)=AH=\frac{SA.AD}{\sqrt{SA^2+AD^2}}=\frac{2a\sqrt{39}}{13}\)