Biết F ( x ) là một nguyên hàm của hàm số f ( x ) = x 8 - x 2 thoả mãn F ( 2 ) = 0 . Khi đó phương trình F ( x ) = x có nghiệm là
A. x = 3
B. x = 1
C. x = -1
D. Tất cả sai
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
F ( x ) = ∫ 1 1 - 3 x + 1 d x = - 1 3 ∫ d ( 1 - 3 x ) 1 - 3 x + x = x - 2 3 1 - 3 x + C
F ( - 1 ) = 2 3 ⇒ C = 3 ⇒ F ( x ) = x - 2 3 1 - 3 x + 3

Chọn A
Đặt t = ln 2 x + 1 ⇒ t 2 = ln 2 x + 1 ⇒ t d t = ln x x d x
∫ ln 2 x + 1 . ln x x d x = ∫ t 2 d t = t 3 3 + C = ln 2 x + 1 3 3 + C
Vì F ( 1 ) = 1 3 nên C = 0
Vậy F 2 ( e ) = 8 9

Chọn A.
∫ x cos x d x = x sin x + cos x + C
F(0) = 1 nên C = 0. Khi đó F(x) = x.sinx + cosx
Do đó g(x) = x.sinx là hàm số chẵn; h(x)=cos x là hàm số chẵn nên F(x)= g(x) + h(x) là hàm số chẵn.

Đáp án A
Phương pháp :
Sử dụng bảng nguyên hàm cơ bản.
Cách giải:
Ta có:
![]()
![]()
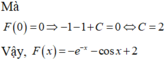
Chọn D
Đặt t = 8 - x 2 ⇒ t 2 = 8 - x 2 ⇒ - t d t = x d x
∫ x 8 - x 2 d x = - ∫ t d t t = - t + C = - 8 - x 2 + C
Vì F ( 2 ) = 0 nên - 8 - 4 + C = 0 suy ra C = 2.
Ta có phương trình - 8 - x 2 + 2 = x ⇔ x = 1 - 3