Tìm điều kiện của các biến để các phân thức sau có nghĩa 2 x 2 + x - 3 x 2 + 5 x + 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{x}{4+2a}\) có nghĩa khi \(a\ne-2\)
\(\dfrac{y}{4-2a}\)có nghĩa khi \(a\ne2\)
\(\dfrac{z}{4-a^2}\)có nghĩa khi \(a\ne\pm2\)
MTC: \(2\left(2+a\right)\left(2-a\right)\)

a. Biểu thức đã cho có nghĩa khi \(\sqrt{x^2-4}\) và \(\sqrt{x-2}\) đồng thời có nghĩa
* \(\sqrt{x^2-4}=\sqrt{\left(x-2\right)\left(x+2\right)}\) có nghĩa khi x \(x\le-2\) hoặc \(x \ge2\)
* \(\sqrt{x-2}\) có nghĩa khi \(x\ge2\)
Vậy điều kiện để biểu thức đã cho có nghĩa là \(x\ge2\)
Với điều kiện trên ta có:
\(\sqrt{x^2-4}+2\sqrt{x-2}=\sqrt{\left(x-2\right)\left(x+2\right)}+2\sqrt{x-2}=\sqrt{x-2}\left(\sqrt{x+2}+2\right)\)

a) ĐK: \(x-5\ne0\Leftrightarrow x\ne5\)
b)
ĐK: \(\left(\dfrac{1}{2}x+4\right)\ne0\Leftrightarrow\dfrac{1}{2}x\ne-4\\ \Leftrightarrow x\ne-8\)
c)ĐK:
\(-2x-10\ne0\\ \Leftrightarrow-2x\ne10\\ \Leftrightarrow x\ne-5\)
a) ĐKXĐ: \(x\ne5\)
b) ĐKXĐ: \(x\ne-8\)
c) ĐKXĐ: \(x\ne-5\)

`sqrt(x-5)` có nghĩa khi:
`x-5 ≥0`
`=> x ≥5`
Vậy `x≥5` thì `sqrt(x-5` có nghĩa
____________
`1/(sqrt(3x-2))` có nghĩa khi
`1/(sqrt(3x-2)) ≥0`
`⇒ 3x-2≥0`
` ⇒3x≥2`
` ⇒x≥2/3`
Vậy `x ≥2/3` thì `1/(sqrt(3x-2))` có nghĩa
Nếu x = 2/3 thì mẫu bằng 0 vậy biểu thức vẫn không có nghĩa thế bài làm vậy là đúng à

Để \(\sqrt{x^2+3}\) có nghĩa thì \(x^2+3\ge0\) (luôn đúng)
Để \(\sqrt{\left(x-1\right)\left(x+2\right)}\) có nghĩa thì \(\left(x-1\right)\left(x+2\right)\ge0\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1\ge0\\x+2\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1\le0\\x+2\le0\end{matrix}\right.\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x\ge1\\x\le-2\end{matrix}\right.\)
a) ĐKXĐ: \(x\in R\)
b) ĐKXĐ: \(\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\)

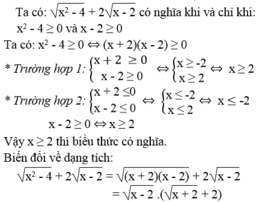
Để phân thức có nghĩa:
x 2 + 5 x + 4 ≠ 0
⇔ (x + 4)(x + 1) ≠ 0
⇔ x ≠ -4, x ≠ -1
Vậy điều kiện để phân thức xác định là x ≠ -4 và x ≠ -1