Giải các phương trình sau: 5x + 16 = 0.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
17 tháng 1 2019
Đặt m = 2 x 2 +x -2
Ta có: 2 x 2 + x - 2 2 +10 x 2 +5x -16 =0
⇔ 2 x 2 + x - 2 2 +5(2 x 2 +x -2) -6 =0
⇔ m 2 +5m -6 =0
Phương trình m 2 +5m -6 = 0 có hệ số a = 1, b = 5, c = -6 nên có dạng
a + b + c = 0
Suy ra : m 1 =1 , m 2 =-6
m1 =1 ta có: 2 x 2 +x -2 =1 ⇔ 2 x 2 +x -3=0
Phương trình 2 x 2 +x -3 = 0 có hệ số a = 2, b = 1 , c = -3 nên có dạng
a +b+c=0
Suy ra: x 1 =1 , x 2 =-3/2
Với m=-6 ta có: 2 x 2 +x -2 = -6 ⇔ 2 x 2 +x +4 =0
∆ = 1 2 -4.2.4 = 1 -32 = -31 < 0 . Phương trình vô nghiệm
Vậy phương trình đã cho có 2 nghiệm : x 1 =1 , x 2 =-32
CX
0
CM
27 tháng 11 2017
Ta có: | - 5x | - 16 = 3x
+ Với x ≥ 0, phương trình tương đương: 5x - 16 = 3x ⇔ 2x = 16 ⇔ x = 8
Thỏa mãn điều kiện x ≥ 0
+ Với x < 0, phương trình tương đương: - 5x - 16 = 3x ⇔ 8x = - 16 ⇔ x = - 2
Thỏa mãn điều kiện x < 0
Vậy phương trình đã cho có tập nghiệm là S = { - 2;8 }
CM
26 tháng 12 2018
Ta có: | - 5x | - 16 = 3x
+ Với x ≥ 0, phương trình tương đương: 5x - 16 = 3x ⇔ 2x = 16 ⇔ x = 8
Thỏa mãn điều kiện x ≥ 0
+ Với x < 0, phương trình tương đương: - 5x - 16 = 3x ⇔ 8x = - 16 ⇔ x = - 2
Thỏa mãn điều kiện x < 0
Vậy phương trình đã cho có tập nghiệm là S = { - 2;8 }
CM
19 tháng 4 2019
a) Phương trình bậc hai
2 x 2 – 7 x + 3 = 0
Có: a = 2; b = -7; c = 3;
Δ = b 2 – 4 a c = ( - 7 ) 2 – 4 . 2 . 3 = 25 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
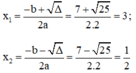
Vậy phương trình có hai nghiệm là 3 và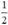 
b) Phương trình bậc hai 6 x 2 + x + 5 = 0
Có a = 6; b = 1; c = 5;
Δ = b 2 – 4 a c = 12 – 4 . 5 . 6 = - 119 < 0
Vậy phương trình vô nghiệm.
c) Phương trình bậc hai 6 x 2 + x – 5 = 0
Có a = 6; b = 1; c = -5;
Δ = b 2 – 4 a c = 12 – 4 . 6 . ( - 5 ) = 121 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
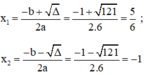
Vậy phương trình có hai nghiệm là -1 và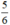 
d) Phương trình bậc hai 3 x 2 + 5 x + 2 = 0
Có a = 3; b = 5; c = 2;
Δ = b 2 – 4 a c = 5 2 – 4 . 3 . 2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
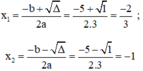
Vậy phương trình có hai nghiệm là -1 và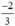 
e) Phương trình bậc hai y 2 – 8 y + 16 = 0
Có a = 1; b = -8; c = 16; Δ = b 2 – 4 a c = ( - 8 ) 2 – 4 . 1 . 16 = 0 .
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép :
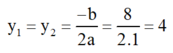
Vậy phương trình có nghiệm kép y = 4.
f) Phương trình bậc hai 16 z 2 + 24 z + 9 = 0
Có a = 16; b = 24; c = 9; Δ = b 2 – 4 a c = 24 2 – 4 . 16 . 9 = 0
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép:
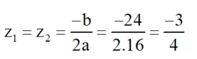
Vậy phương trình có nghiệm kép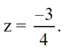 
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt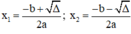 
+ Nếu Δ = 0, phương trình có nghiệm kép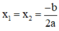 
;
+ Nếu Δ < 0, phương trình vô nghiệm.
PT
1
CM
13 tháng 3 2018
b) x 4 - 5 x 2 + 4 = 0
Đặt t = x 2 ≥ 0 , ta có phương trình:
t 2 - 5t + 4 = 0 (dạng a + b + c = 1 -5 + 4 = 0)
t 1 = 1 (nhận) ; t 2 = 4 (nhận)
với t = 1 ⇔ x 2 = 1 ⇔ x = ± 1
với t = 4 ⇔ x 2 = 4 ⇔ x = ± 2
Vậy nghiệm của phương trình x = ±1; x = ± 2
25 tháng 1 2018
a, pt <=> (x^3+x^2)-(4x^2-4) = 0
<=> (x+1).(x^2-4x+4) = 0
<=> (x+1).(x-2)^2 = 0
<=> x+1=0 hoặc x-2=0
<=> x=-1 hoặc x=2
b, pt <=> (x^4-x^3)+(2x^3-2x^2)-(2x^2-2x)+(3x-3) = 0
<=> (x-1).(x^3+2x^2-2x+3) = 0
<=> (x-1).[(x^3+3x^2)-(x^2+3x)+(3x+3)] = 0
<=> (x-1).(x+3).(x^2-3x+3) = 0
<=> x-1=0 hoặc x+3=0 ( vì x^2-3x+3 > 0 )
<=> x=1 hoặc x=-3
c, pt <=> (4^x-10.2^x+25)-9 =0
<=> (2^x-5)^2-9 = 0
<=> (2^x-5-3).(2^x-5+3) = 0
<=> (2^x-8).(2^x-2) = 0
<=> 2^x-8=0 hoặc 2^x-2=0
<=> x=3 hoặc x=1
Tk mk nha
KT
25 tháng 1 2018
a) \(x^3-3x^2+4=0\)
\(\Leftrightarrow\)\(x^3+x^2-4x^2+4=0\)
\(\Leftrightarrow\)\(x^2\left(x+1\right)-4\left(x-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\)\(\left(x+1\right)\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow\)\(\left(x+1\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x+1=0\\x-2=0\end{cases}}\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=-1\\x=2\end{cases}}\)
Vậy....
5x + 16 =0
⇔ 5x = -16
⇔
.
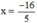Vậy phương trình có nghiệm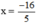
.