
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có:Δ =(-7)2 -4.2.2 =49 -16 =33 >0
Phương trình có 2 nghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =7/2 ;x1x2 =c/a =2/2 =1
b) c = -16 suy ra ac < 0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 =-b/a =-2/5 ;x1x2 =c/a =-16/5
c) Ta có: Δ’ = 22 – (2 -√3 )(2 + √2 ) =4 -4 - 2√2 +2√3 +√6
= 2√3 - 2√2 +√6 >0
Phương trình 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
d) Ta có : Δ = (-3)2 -4.1,4.1,2 =9 – 6,72 =2,28 >0
Phương trình có 2 ghiệm phân biệt .Theo hệ thức Vi-ét, ta có:
x1 + x2 = -b/a = 3/(1.4) = 30/14 = 15/7 ; x1x2 = c/a = (1.2)/(1.4) = 12/14 = 6/7
Ta có: Δ = 12 -4.5.2 = 1 - 40 = -39 < 0

a) Phương trình 4 x 2 + 2 x − 5 = 0
Có a = 4; b = 2; c = -5, a.c < 0
⇒ Phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-et ta có: 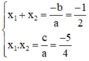
b) Phương trình . 9 x 2 − 12 x + 4 = 0
Có a = 9; b' = -6; c = 4 ⇒ Δ 2 = ( - 6 ) 2 - 4 . 9 = 0
⇒ Phương trình có nghiệm kép x 1 = x 2 .
Theo hệ thức Vi-et ta có: 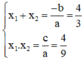
c) Phương trình 5 x 2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 1 2 − 4.2.5 = − 39 < 0
⇒ Phương trình vô nghiệm.
d) Phương trình 159 x 2 − 2 x − 1 = 0
Có a = 159; b = -2; c = -1; a.c < 0
⇒ Phương trình có hai nghiệm phân biệt x 1 ; x 2 .
Theo hệ thức Vi-et ta có: 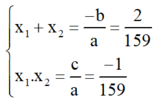

5x2 – 20 = 0
⇔ 5x2 = 20
⇔ x2 = 4
⇔ x = 2 hoặc x = -2.
Vậy phương trình có hai nghiệm x = 2 và x = -2.

a) Phương trình bậc hai: 7 x 2 – 2 x + 3 = 0
Có: a = 7; b = -2; c = 3; Δ = b 2 – 4 a c = ( - 2 ) 2 – 4 . 7 . 3 = - 80 < 0
Vậy phương trình vô nghiệm.
b) Phương trình bậc hai 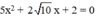
Có: a = 5; b = 2√10; c = 2; Δ = b 2 – 4 a c = ( 2 √ 10 ) 2 – 4 . 2 . 5 = 0
Vậy phương trình có nghiệm kép.
c) Phương trình bậc hai 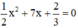
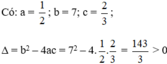
Vậy phương trình có hai nghiệm phân biệt.
d) Phương trình bậc hai 1 , 7 x 2 – 1 , 2 x – 2 , 1 = 0
Có: a = 1,7; b = -1,2; c = -2,1;
Δ = b 2 – 4 a c = ( - 1 , 2 ) 2 – 4 . 1 , 7 . ( - 2 , 1 ) = 15 , 72 > 0
Vậy phương trình có hai nghiệm phân biệt.
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt 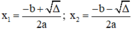
+ Nếu Δ = 0, phương trình có nghiệm kép 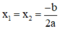 ;
;
+ Nếu Δ < 0, phương trình vô nghiệm.

a. Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2}{5}\\x_1x_2=-\dfrac{7}{5}\end{matrix}\right.\)
b.
\(A=x_1^2+x_2^2-x_1x_2=\left(x_1+x_2\right)^2-3x_1x_2\)
\(=\left(\dfrac{2}{5}\right)^2-3\left(-\dfrac{7}{5}\right)=\dfrac{109}{25}\)

Phương trình 5x2 + x + 2 = 0
Có a = 5; b = 1; c = 2 ⇒ Δ = 12 – 4.2.5 = -39 < 0
⇒ Phương trình vô nghiệm.

Phương trình 5x2 + 2x -16 =0 có hệ số a=5 ,b=2 c=-16
Ta có: Δ'=12 -5(-16) = 1 + 80 =81 >0
Δ' = 81 =9
Phương trình 3x2 -2x -5 =0 có hệ số a =3,b = -2, c = -5
Ta có: Δ'=(-1)2 -3(-5) = 1 + 15 =16 >0
Δ' = 16 =4
Phương trình 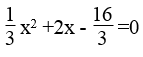
Δ'=32 -1(-16) = 9 +16 =25 > 0
Δ' = 25 =5
Phương trình 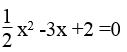
Ta có: Δ'=(-3)2 -1.4 = 9 -4 =5 >0
Δ' = 5

5x2 – 3x + 1 = 2x + 11
⇔ 5x2 – 3x + 1 – 2x – 11 = 0
⇔ 5x2 – 5x – 10 = 0
Có a = 5; b = -5; c = -10 ⇒ a - b + c = 0
⇒ Phương trình có hai nghiệm: x1 = -1 và x2 = -c/a = 2.
Vậy phương trình có tập nghiệm S = {-1; 2}.

x4 – 5x2 + 4 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t2 – 5t + 4 = 0 (2)
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t1 = 1; t2 = c/a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.

Phương trình bậc hai 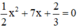
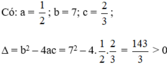
Vậy phương trình có hai nghiệm phân biệt.
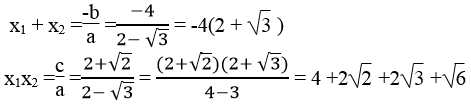

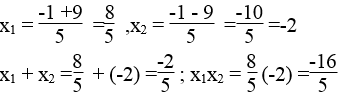
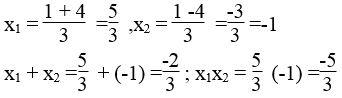
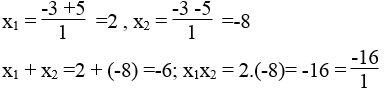
cho mk một tk đi bà con ơi
ủng hộ mk đi làm ơn
Dùng \(\Delta\)ra ngay nha bạn.