K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
26 tháng 12 2018
Ta có: | - 5x | - 16 = 3x
+ Với x ≥ 0, phương trình tương đương: 5x - 16 = 3x ⇔ 2x = 16 ⇔ x = 8
Thỏa mãn điều kiện x ≥ 0
+ Với x < 0, phương trình tương đương: - 5x - 16 = 3x ⇔ 8x = - 16 ⇔ x = - 2
Thỏa mãn điều kiện x < 0
Vậy phương trình đã cho có tập nghiệm là S = { - 2;8 }
18 tháng 4 2019
\(|-5x|=3x-16\)
\(TH1:-5x=3x-16\Leftrightarrow-8x=-16\Leftrightarrow x=2\)
\(TH2:-5x=-3x+16\Leftrightarrow-2x=16\Leftrightarrow x=-8\)
CM
3 tháng 5 2017
a) (*) ⇔ (5x – 3)2 – (4x – 7)2 = 0
⇔ (5x – 3 + 4x – 7)(5x – 3 – 4x + 7) = 0
⇔ (9x – 10)(x + 4) = 0 ⇔ 9x – 10 = 0 hoặc x + 4 = 0
⇔ x = 10/9 hoặc x = -4
Tập nghiệm : S = { 10/9 ; -4}
b) ĐKXĐ: (x + 4)(x – 4) ≠ 0 ⇔ x + 4 ≠ 0 và x – 4 ≠ 0 ⇔ x ≠ ⇔ 4
Ta có: x2 – 16 = (x + 4)(x – 4) ≠ 0
Quy đồng và khử mẫu, ta được:
96 + 6(x2 – 16) = (2x – 1)(x – 4) + (3x – 1)(x + 4)
⇔ 96 + 6x2 – 96 = 2x2 – 8x – x + 4 + 3x2 + 12x – x – 4
⇔ x2 – 2x = 0 ⇔ x(x – 2) = 0
⇔ x = 0 hoặc x – 2 = 0
⇔ x = 0 hoặc x = 2 (thỏa mãn ĐKXĐ)
Tập nghiệm: S = {0;2}
c) ĐKXĐ: x ≠ 0; x – 1 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ 0; x ≠ 1 và x ≠ 2
MTC: 4x(x – 2)(x – 1)
Quy đồng và khử mẫu, ta được:
2(1 – x)(x – 1) – x(x – 2) = 2(x – 1)2 – 2(x – 1)(x – 2)
⇔ -2x2 + 4x – 2 – x2 + 2x = 2x2 – 4x + 2 – 2x2 + 6x – 4
⇔ 3x2 – 4x = 0 ⇔ x(3x – 4) = 0 ⇔ x = 0 hoặc x = 4/3
(x = 0 không thỏa mãn ĐKXĐ)
Tập nghiệm: S = {4/3}
CM
8 tháng 9 2019
|-5x| - 16 = 3x (4)
Ta có: |-5x| = -5x khi -5x ≥ 0 hay x ≤ 0.
|-5x| = -(-5x) = 5x khi -5x < 0 hay x > 0.
Vậy phương trình (4) tương đương với:
+ -5x – 16 = 3x với điều kiện x ≤ 0.
-5x – 16 = 3x ⇔ -5x – 3x = 16 ⇔ -8x = 16 ⇔ x = -2.
Giá trị x = -2 thỏa mãn điều kiện x ≤ 0 nên là nghiệm của (4).
+ 5x – 16 = 3x với điều kiện x > 0.
5x – 16 = 3x ⇔ 5x – 3x = 16 ⇔ 2x = 16 ⇔ x = 8
Giá trị x = 8 thỏa mãn điều kiện x > 0 nên là nghiệm của (4).
Vậy phương trình (4) có nghiệm x = -2 và x = 8.
.
.
PT
1
CM
12 tháng 2 2018
(2 – 3x)(x + 11) = (3x – 2)(2 – 5x)
⇔ (2 – 3x)(x + 11) – (3x – 2)(2 – 5x) = 0
⇔ (2 – 3x)(x + 11) + (2 – 3x)(2 – 5x) = 0
⇔ (2 – 3x)[(x + 11) + (2 – 5x)] = 0
⇔ (2 – 3x)(x + 11 + 2 – 5x) = 0
⇔ (2 – 3x)(13 – 4x) = 0 ⇔ 2 – 3x = 0 hoặc 13 – 4x = 0
2 – 3x = 0 ⇔ x = 2/3
13 – 4x = 0 ⇔ x = 13/4
Vậy phương trình có nghiệm x = 2/3 hoặc x = 13/4
19 tháng 8 2021
1: Ta có: \(\dfrac{3}{x-3}+\dfrac{4}{x+3}=\dfrac{3x-7}{x^2-9}\)
\(\Leftrightarrow\dfrac{3x+9}{\left(x-3\right)\left(x+3\right)}+\dfrac{4x-12}{\left(x-3\right)\left(x+3\right)}=\dfrac{3x-7}{\left(x-3\right)\left(x+3\right)}\)
Suy ra: \(3x+9+4x-12=3x-7\)
\(\Leftrightarrow4x=-7+12-9=-4\)
hay \(x=-1\left(nhận\right)\)
2: Ta có: \(\dfrac{3}{x-4}-\dfrac{4}{x+4}=\dfrac{3x-4}{x^2-16}\)
\(\Leftrightarrow\dfrac{3x+12}{\left(x-4\right)\left(x+4\right)}-\dfrac{4x-16}{\left(x+4\right)\left(x-4\right)}=\dfrac{3x-4}{\left(x-4\right)\left(x+4\right)}\)
Suy ra: \(3x+12-4x+16=3x-4\)
\(\Leftrightarrow28-4x=-4\)
\(\Leftrightarrow4x=32\)
hay \(x=8\left(tm\right)\)
19 tháng 8 2021
3: Ta có: \(\dfrac{5x^2-12}{x^2-1}+\dfrac{3}{x-1}=\dfrac{5x}{x+1}\)
Suy ra: \(5x^2-12+3x+3=5x^2-5x\)
\(\Leftrightarrow3x-9+5x=0\)
\(\Leftrightarrow8x=9\)
hay \(x=\dfrac{9}{8}\left(nhận\right)\)
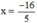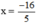Ta có: | - 5x | - 16 = 3x
+ Với x ≥ 0, phương trình tương đương: 5x - 16 = 3x ⇔ 2x = 16 ⇔ x = 8
Thỏa mãn điều kiện x ≥ 0
+ Với x < 0, phương trình tương đương: - 5x - 16 = 3x ⇔ 8x = - 16 ⇔ x = - 2
Thỏa mãn điều kiện x < 0
Vậy phương trình đã cho có tập nghiệm là S = { - 2;8 }