giải câu 20,21 thôi ạ 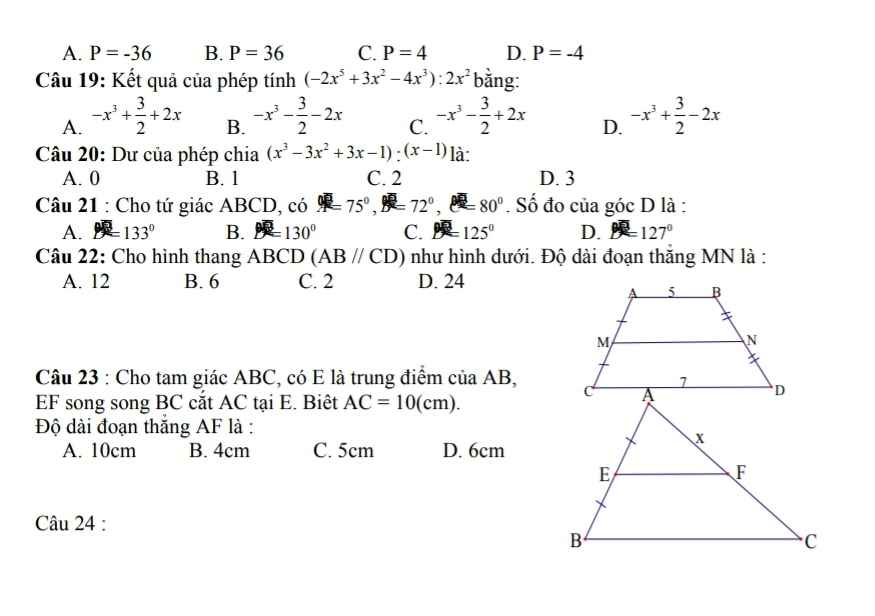
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


20: Ta có: \(A=\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{x}-1}\right):\left(\dfrac{\sqrt{x}+2}{\sqrt{x}-1}-\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\right)\)
\(=\dfrac{-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-4-x+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}-2}{3\sqrt{x}}\)

A=(m + 20,21) + ( m + 20,21) + (m + 20,21) + (n + 20,21) + (n + 20,21) + (n + 20,21)
= 3(m + 20,21) + 3(n + 20,21)
= 3(m+n + 20,21x2)
Khi m = 20,21 - n thay vào ta được
A =3(20,21 - n +n +20,21x2)
=3(3x20,21)
=9x20,21
=189
A=(m + 20,21) + ( m + 20,21) + (m + 20,21) + (n + 20,21) + (n + 20,21) + (n + 20,21)
= 3(m + 20,21) + 3(n + 20,21)
= 3(m+n + 20,21x2)
Khi m = 20,21 - n thay vào ta được
A =3(20,21 - n +n +20,21x2)
=3(3x20,21)
=9x20,21
=189

=20,21*(4,8-3,7)-20,21
=20,21*1,1-20,21
=20,21*0,1
=2,021

3. She said I should ask a lawyer.
4. Mrs Linh asked me to give Tuan this book.

a: Xét tứ giác OEAF có
\(\widehat{OEA}+\widehat{OFA}=180^0\)
Do đó: OEAF là tứ giác nội tiếp

a: Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
nen AMHN là hình chữ nhật
Xét tứ giác MHDN có
MH//DN
MH=DN
Do đó: MHDN là hình bình hành
b: Xét tứ giác AHDK có
N là trug điểm chung của AD và HK
AD vuông góc với HK
Do đó: AHDK là hình thoi


Câu 20:
a) Xét (O) có
CM là tiếp tuyến có M là tiếp điểm(gt)
CA là tiếp tuyến có A là tiếp điểm(gt)
Do đó: CM=CA(Tính chất hai tiếp tuyến cắt nhau)
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm(gt)
DB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: DM=DB(Tính chất hai tiếp tuyến cắt nhau)
Ta có: CM+MD=CD(M nằm giữa C và D)
mà CM=CA(cmt)
và MD=DB(cmt)
nên CD=AC+BD(đpcm)
b) Xét (O) có
CM là tiếp tuyến có M là tiếp điểm(gt)
CA là tiếp tuyến có A là tiếp điểm(gt)
Do đó: OA là tia phân giác của \(\widehat{AOM}\)(Tính chất hai tiếp tuyến cắt nhau)
hay \(\widehat{AOM}=2\cdot\widehat{COM}\)
Xét (O) có
DM là tiếp tuyến có M là tiếp điểm(gt)
DB là tiếp tuyến có B là tiếp điểm(gt)
Do đó: OD là tia phân giác của \(\widehat{MOB}\)(Tính chất hai tiếp tuyến cắt nhau)
hay \(\widehat{MOB}=2\cdot\widehat{MOD}\)
Ta có: \(\widehat{AOM}+\widehat{BOM}=180^0\)(hai góc kề bù)
mà \(\widehat{AOM}=2\cdot\widehat{COM}\)(cmt)
và \(\widehat{MOB}=2\cdot\widehat{MOD}\)(cmt)
nên \(2\cdot\widehat{COM}+2\cdot\widehat{DOM}=180^0\)
\(\Leftrightarrow\widehat{COM}+\widehat{DOM}=90^0\)
hay \(\widehat{COD}=90^0\)
Vậy: \(\widehat{COD}=90^0\)
c) Ta có: CA=CM(cmt)
nên C nằm trên đường trung trực của AM(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: OA=OM(=R)
nên O nằm trên đường trung trực của AM(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra OC là đường trung trực của AM
⇔OC⊥AM
mà OC cắt AM tại I(gt)
nên OC⊥AM tại I
hay \(\widehat{OIM}=90^0\)
Ta có: DM=DB(cmt)
nên D nằm trên đường trung trực của BM(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OM(=R)
nên O nằm trên đường trung trực của BM(Tính chất đường trung trực của một đoạn thẳng)(4)
Từ (3) và (4) suy ra OD là đường trung trực của BM
⇔OD⊥BM
mà OD cắt BM tại K(gt)
nên OD⊥BM tại K
hay \(\widehat{OKM}=90^0\)
Ta có: \(\widehat{COD}=90^0\)(cmt)
mà I∈CO(gt)
và K∈OD(gt)
nên \(\widehat{IOK}=90^0\)
Xét tứ giác IOKM có
\(\widehat{IOK}=90^0\)(cmt)
\(\widehat{OKM}=90^0\)(cmt)
\(\widehat{OIM}=90^0\)(cmt)
Do đó: IOKM là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)


 giải câu d thôi ạ
giải câu d thôi ạ

 20,21 ạ
20,21 ạ
20. D
21. A
20 - D
21 - A