Cho tam giác ABC có a = 8 cm, b = 9 cm, c = 10 cm. Tam giác ABC là
A. Tam giác nhọn
B. Tam giác tù
C. Tam giác vuông
D. Tam giác đều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
15 tháng 4 2022
a: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có
góc C chung
Do đó: ΔCDA\(\sim\)ΔCEB
b: Xét ΔHEA vuông tại E và ΔHDB vuông tại D có
\(\widehat{AHE}=\widehat{BHD}\)
Do đó: ΔHEA\(\sim\)ΔHDB
Suy ra: HE/HD=HA/HB
hay \(HE\cdot HB=HD\cdot HA\)
27 tháng 3 2022
ok, thanks nhưng dừng khoảng chừng là 2 giây, you lấy từ qanda
17 tháng 9 2023
a) Tam giác ABC nhọn:
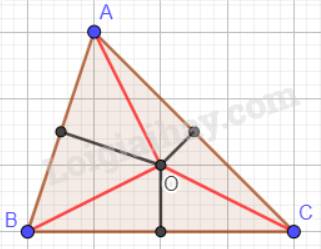
b) Tam giác ABC vuông tại A:
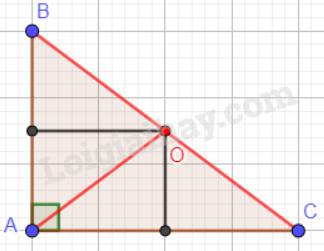
c) Tam giác ABC có góc A tù:
24 tháng 3 2022
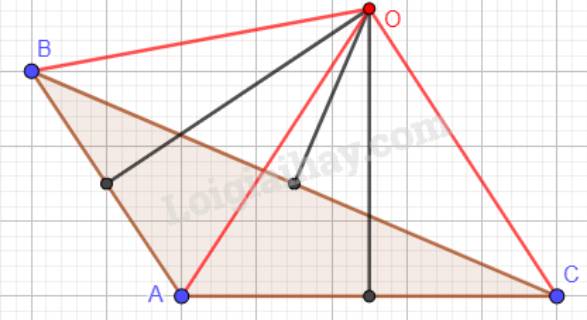
-Lưu ý: Chỉ mang tính chất tóm tắt bài làm, bạn không nên trình bày theo nhé!
a) △ABD và △EBD có: \(\widehat{ABD}=\widehat{EBD}\) (BD là tia phân giác của \(\widehat{ABC}\)) ; BD là cạnh chung ; \(\widehat{BAD}=\widehat{BED}=90^0\)
\(\Rightarrow\)△ABD=△EBD (c-g-c).
b) △ABD=△EBD (cmt) \(\Rightarrow AB=EB\) \(\Rightarrow\)△ABE cân tại B mà \(\widehat{ABC}=60^0\)
\(\Rightarrow\)△ABE đều.
c) \(\widehat{BAE}+\widehat{EAC}=90^0\Rightarrow60^0+\widehat{EAC}=90^0\Rightarrow\widehat{EAC}=30^0\)
\(\widehat{ABE}+\widehat{ACE}=90^0\Rightarrow60^0+\widehat{ACE}=90^0\Rightarrow\widehat{ACE}=30^0=\widehat{EAC}\)
\(\Rightarrow\)△AEC cân tại E. \(\Rightarrow AE=EC=AB=BE\)
\(\Rightarrow\)E là trung điểm BC và \(AB=\dfrac{1}{2}BC\)
\(\Rightarrow BC=10 \left(cm\right)\)
8 tháng 2 2022
a. Áp dụng định lý pitago, ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AC=\sqrt{10^2-6^2}=\sqrt{64}=8cm\)
\(C_{ABC}=6+8+10=24cm\)
b. xét tam giác vuông ABD và tam giác vuông BDM, có:
B : góc chung
AD: cạnh chung
Vậy tam giác vuông ABD = tam giác vuông BDM ( cạnh huyền - góc nhọn )
CC
15 tháng 12 2019
\(\Delta ABC\)có \(\widehat{A}=60^o\)\(\Rightarrow\widehat{B}+\widehat{C}=120^o\)
mà \(\widehat{B}=3.\widehat{C}\)\(\Rightarrow4.\widehat{C}=120^o\)\(\Rightarrow\widehat{C}=30^o\)\(\Rightarrow\widehat{B}=90^o\)
\(\Rightarrow\Delta ABC\)vuông tại B
Ta có: cosC = a 2 + b 2 − c 2 2 a b = 8 2 + 9 2 − 10 2 2.8.9 > 0
⇒ 0 0 < C ^ < 90 0
Tam giác ABC có AB = c là cạnh lớn nhất. Do đó, góc C là góc lớn nhất.
Lại có: 0 0 < C ^ < 90 0 nên tam giác ABC là tam giác nhọn.
Chọn A