Cho hình chóp S.ABC có ASB ^ = BSC ^ = ASC ^ = 60 0 và SA = 2 , SB = 3 , SC = 4 . Tính thể tích khối chóp S.ABC
A. 2 2
B. 2 2 3
C. 2 3
D. 2 3 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn đáp án B.
Ta có: S A ⊥ S B S A ⊥ S C ⇒ S A ⊥ ( S B C )
Vì vậy áp dụng công thức cho trường hợp khối chóp có cạnh bên vuông góc đáy có:
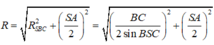
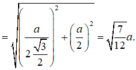

Chọn A
Trên cạnh SB, SC lần lượt lấy các điểm M, N thỏa mãn SM = SN = 1.
Ta có AM = 1, AN = 2 , MN = 3
=> tam giác AMN vuông tại A
Hình chóp S.AMN có SA = SM = SN = 1.
=> hình chiếu của S trên (AMN) là tâm I của đường tròn ngoại tiếp tam giác AMN, ta có I là trung điểm của MN
Trong
∆
SIM, 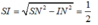
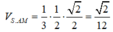
Ta có 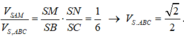

Đáp án D
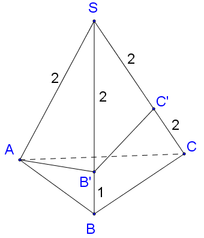
Gọi B ' , C ' lần ượt là hai điểm thuộc SB, SC sao cho S B ' = S C ' = 2
Xét tứ diện S . A B ' C ' có A S B ' ⏜ = B ' S C ' ⏜ = C ' S A ⏜ = 60 ° S A = S B ' = S C ' = 2 ⇒ S . A B ' C ' là tứ diện đều cạnh 2
Khi đó V S . A B ' C ' = S A 3 2 12 = 2 3 2 12 = 2 2 3
mà V S . A B ' C ' V S . A B C = S B ' S B . S C ' S C = 2 3 . 2 6 = 2 9 .
Vậy V S . A B C = 3 2