Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta chọn (SBC) làm mặt đáy => chiều cao khối chóp là d(A, (SBC)) = 3a
Tam giác SBC vuông cân tại S nên ![]()
Vậy thể tích khối chóp ![]()
Chọn A.

Đáp án D
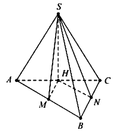
Gọi H là hình chiếu của S trên A C ⇒ S H ⊥ A B C
Kẻ H M ⊥ A B M ∈ A B , H N ⊥ A C N ∈ A C
Suy ra S A B ; A B C ^ = S B C ; A B C ^ = S M H ^ = S N H ^ = 60 °
⇒ ∆ S H M = ∆ S H N ⇒ H M = H N ⇒ H là trung điểm của AC
Tam giác SHM vuông tại H, có tan S M H ^ = S H H M ⇒ S H = a 3 2
Diện tích tam giác ABC là S ∆ A B C = 1 2 . A B . B C = a 2 2
Vậy thể tích cần tính là V = 1 3 . S H . S A B C = 1 3 . a 3 2 . a 2 2 = a 3 3 12

Đáp án D
Ta có: V S . A B C D = 1 3 S A . S A B C = 1 3 . a 3 . a 2 3 4 = a 3 4

Trong (SBC) qua G kẻ M N / / B C M ∈ S B ; N ∈ S C . Khi đó mặt phẳng đi qua AG và song song với BC chính là mặt phẳng (AMN). Mặt phẳng này chia khối chóp thành 2 khối S.AMN và AMNBC.
Gọi H là trung điểm của BC.
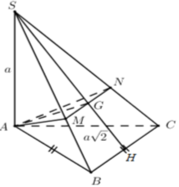
Vì M N / / B C
Theo định lí Ta-lét ta có:
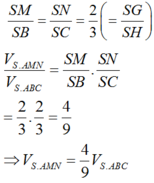
Mà
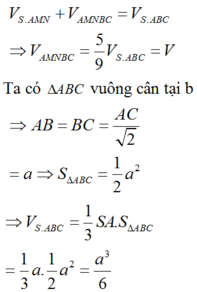
Vậy
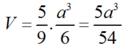
Chọn A.

Chọn B
Gọi M là điểm trên đoạn SC sao cho SC=3SM Tính được AB=BM=a, A M = a 2 =>DABM vuông tại B, suy ra trung điểm H của AM là tâm đường tròn ngoại tiếp DABM. Suy ra
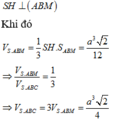

Đáp án B
Gọi O là hình chiếu của S lên A B C ; S O = S B 2 − B O 2 = 4 a 2 − a 2 3 = a 33 3
V = 1 3 S Δ A B I . S O = 1 3 . a 2 3 8 . a 33 3 = a 3 11 24


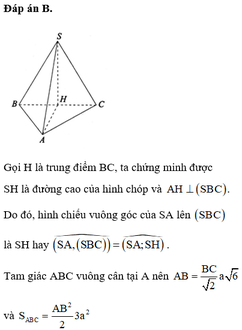
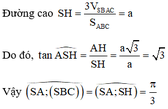
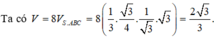
Đáp án C