Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bán kính mặt cầu ngoại tiếp hình chóp đã cho là R = \(\dfrac{1}{2}\sqrt{a^2+b^2+c^2}\).
Diện tích mặt cầu cần tìm là S = 4\(\pi\)R2 = (a2+b2+c2)\(\pi\).
Thể tích khối cầu cần tìm là V = 4/3.\(\pi\)R3 = \(\dfrac{\pi}{6}\sqrt{a^2+b^2+c^2}^3\).

+)Gọi H là chân đường cao hạ từ A - -> BC
Tam giác AHC vuông tại H nên
AH = √(a² -a²/4) = a√3/2
Diện tích tam giác ABC là S(ABC) = 1/2.AH.BC= 1/2.a²√3/2
(dvdt)
+)Từ S hạ SK ┴ AH , Kết hợp AH ┴ BC ta có SK ┴ (ABC)
Hay SK là đường cao của hình chóp đều SABC
+) Bài cho góc giữa các mặt bên với đáy là 60 độ nên
góc giữa (SH,HK) = 60 độ
Tam giác vuông SKH có SK = HK.tan(60)
Tam giác vuông BKH có HK = a/2.tan(30) = a√3/6
- - > SK = a√3/6.tan(60) = a/2
Vậy V(SABC) =1/3.SK.S(ABC) = 1/3.a/2.1/2.a²√3/2
= a³√3/24 (dvtt)

Lời giải:
Gọi $H$ là chân đường cao kẻ từ $S$ xuống mặt phẳng $(ABC)$
Ta có \(\left\{\begin{matrix} SH\perp AB\\ SA\perp AB\end{matrix}\right.\Rightarrow AB\perp (SHA)\rightarrow AB\perp HA\)
Tương tự \(BC\perp HC\). Kết hợp với \(ABC\) vuông cân tại $B$ suy ra \(ABCH\) là hình vuông
Có \(AH\parallel (SBC)\Rightarrow d(A,(SBC))=d(H,(SBC))\)
Kẻ \(HT\perp SC\). Có \(\left\{\begin{matrix} SH\perp BC\\ HC\perp BC\end{matrix}\right.\Rightarrow BC\perp (SHC)\Rightarrow BC\perp HT\)
Do đó \(HT\perp (SBC)\Rightarrow d(H,(SBC))=HT=\sqrt{\frac{SH^2.HC^2}{SH^2+HC^2}}=\sqrt{\frac{SH^2.AB^2}{SH^2+AB^2}}=\sqrt{2}\Rightarrow SH=\sqrt{6}a\)
Từ trung điểm $O$ của $AC$ dựng trục vuông góc với mặt phẳng $(ABC)$. Trên trục đó ta lấy điểm $I$ là tâm mặt cầu ngoại tiếp.
\(IS^2=IA^2=IH^2\Leftrightarrow (\overrightarrow{IO}+\overrightarrow{OH}+\overrightarrow{HS})^2=IO^2+OH^2\)
\(\Leftrightarrow HS^2+2\overrightarrow{IO}.\overrightarrow{HS}=0\)
Do \(\overrightarrow {SH}\parallel \overrightarrow {IO}\Rightarrow \overrightarrow {IO}=k\overrightarrow{SH}\). Thay vào PT trên có $k=\frac{1}{2}$
\(\Rightarrow IO=\frac{\sqrt{6}a}{2}\Rightarrow IA=\sqrt{IO^2+AO^2}=\sqrt{3}a\)
\(\Rightarrow S_{\text{mặt cầu}}=4\pi R^2=12a^2\pi\)
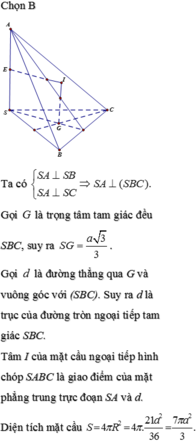
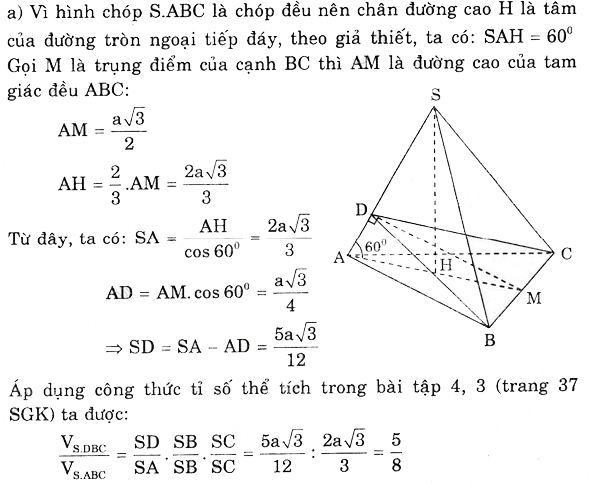

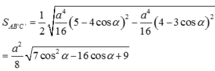
Chọn đáp án B.
Ta có: S A ⊥ S B S A ⊥ S C ⇒ S A ⊥ ( S B C )
Vì vậy áp dụng công thức cho trường hợp khối chóp có cạnh bên vuông góc đáy có: