Trong quá trình truyền tải điện, điện năng bị hao phí phần lớn ở
A. đường dây
B. thiết bị đo
C. nơi tiêu thụ
D. trạm phát điện
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 tháng 6 2016
Hao phí truyền tải điện: \(P_{hp}=10\%.P= 0,1.P=20kW=20000W\)
Ta có: \(P_{hp}=I^2.R=I^2.200=20000\Rightarrow I = 10A\)
Chọn A.
VT
19 tháng 3 2017
Chọn D
H 1 =1-D P 1 / P 1 => 1- H 1 =D P 1 / P 1 = P 1 .R/ ( U cos φ ) 2
H 2 =1-D P 2 / P 2 => 1- H 2 =D P 2 / P 2 = P 2 .R/ ( U cos φ ) 2
ð(1- H 1 )/(1- H 2 ) = P 1 / P 2
ð P 1 = P 0 + ∆ P 1 và P 2 = 1 , 25 P 0 + ∆ P 2
ð P 1 / P 2 = H 2 / 1 , 25 H 1
ð(1- H 1 )/(1- H 2 ) = H 2 / 1 , 25 H 1
ð(1-0,82)/(1- H 2 ) = H 2 / 1 , 25 . 0 , 82
ð H 2 2 - H 2 + 0,1845 = 0 ( H 2 >70%)
ð H 2 =75,6%
VT
1 tháng 11 2017
Đáp án D
+ Ban đầu: công suất trạm phát P, hao phí ∆P, tiêu thụ Ptt
+ Lúc sau: công suất trạm phát P’ = kP; hao phí 
; tiêu thụ Ptt'
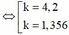
=> loại k = 4,2 và chọn k = 1,356.
Có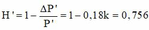
VT
4 tháng 5 2017
Đáp án A
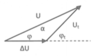
Gọi P, P t , DP là công suất trạm phát, công suất nơi tiêu thụ và công suất hao phí; U, U t , DU là điện áp trạm phát, điện áp nơi tiêu thụ và độ giảm áp.
- Ban đầu: P t = 0,8P Þ DP = 0,2P; cosjt = 0,8 Þ cos a = -0,8 (hình vẽ, góc bù).
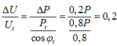
Sau đó:
VT
3 tháng 10 2018
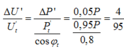
Đáp án C
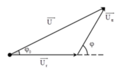
+ Ta có giản đồ vecto cho các điện áp
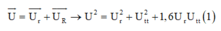
+ Mặc khác kết hợp với giả thuyết
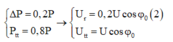
+ Thay hệ trên vào (1) ta tìm được cos φ = 5 34
+ Để giảm hao phí xuống 4 lần, nghĩa là I giảm 2 lần do vậy U r = I r cũng giảm đi hai lần
+Áp dụng định lý sin trong tam giác
VT
20 tháng 9 2019
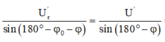
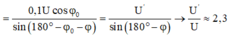
Giải thích: Đáp án A
Phương pháp:Sử dụng giản đồ vecto
Công thức tính công suất và hiệu suất
Lí thuyết về truyền tải điện năng đi xa
Cách giải: Ta có: cosφ' = 0,8
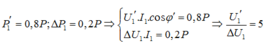
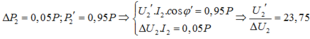
Sử dụng định lí hàm số cos:
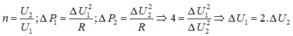
Chuẩn hoá số liệu: Cho ∆U1 = 1 => U1’ = 5
VT
4 tháng 3 2018
Đáp án A
Phương pháp:Sử dụng giản đồ vecto
Công thức tính công suất và hiệu suất
Lí thuyết về truyền tải điện năng đi xa
Cách giải: Ta có: cos
φ
'
= 0,8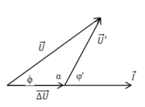 
Sử dụng định lí hàm số cos:
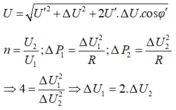
Chuẩn hoá số liệu: Cho ∆ U 1 = 1
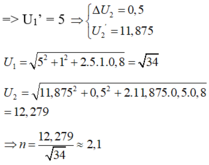
Đáp án A
Trong quá trình truyền tải điện năng đi xa, điện năng bị hao phí phần lướn ở đường dây truyền tải