Giải tam giác ABC vuông tại A, biết rằng a = 20 c m , B ^ = 35 o
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 2 2018
(Lưu ý: ΔABC vuông tại A nên ∠ B + ∠ C = 90 °
Giải tam giác tức là đi tìm số đo các cạnh và các góc còn lại.)
a)
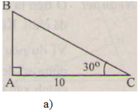
∠ B = 90 o - ∠ C = 90 ° - 30 ° = 60 °
c = b . t g C = 10 . t g 30 ° ≈ 5 , 77 ( c m )
b)
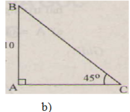
∠ B = 90 ° - ∠ C = 90 ° - 45 ° = 45 °
=> ΔABC cân => b = c = 10 (cm)
c)
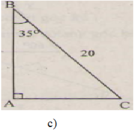
∠ B = 90 o - ∠ C = 90 ° - 35 ° = 55 ° b = a sin B = 20 . sin 35 ° ≈ 11 , 47 ( c m ) c = a sin C = 20 . sin 55 ° ≈ 16 , 38 ( c m )
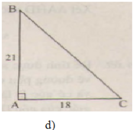
d)
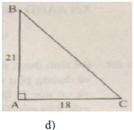
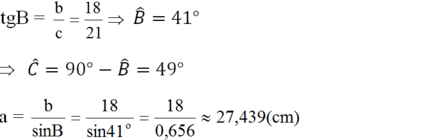
(Ghi chú: Bạn nên sử dụng các kí hiệu cạnh là a, b, c (thay vì BC, AC, AB) để đồng bộ với đề bài đã cho.
Cách để nhớ các cạnh là: cạnh nào thiếu chữ cái nào thì chữ cái đó là kí hiệu của cạnh đó. Ví dụ: cạnh AB thiếu chữ cái C nên c là kí hiệu của cạnh.
hoặc cạnh đối diện với góc nào thì đó chính là kí hiệu của cạnh. Ví dụ: cạnh đối diện với góc B là cạnh b (chính là cạnh AC))
PT
1
CM
7 tháng 11 2019
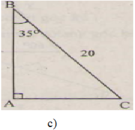
∠B = 90o - ∠C = 90o - 35o = 55o
b = asinB = 20.sin35o ≈ 11,47 (cm)
c = asinC = 20.sin55o ≈ 16,38 (cm)
D
Giải các tam giác vuông sau, tầm giác ABC vuông tại A biết: a)a=20;b=16 b)b=10;C=50° c)cos B=3/4;c=5
2
15 tháng 10 2023
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AB=\sqrt{20^2-16^2}=12\)
Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{3}{5}\)
=>\(\widehat{C}\simeq37^0\)
=>\(\widehat{B}=90^0-37^0=53^0\)
b: ΔABC vuông tại A
=>\(\widehat{B}+\widehat{C}=90^0\)
=>\(\widehat{B}=40^0\)
Xét ΔABC vuông tại A có
\(tanC=\dfrac{AB}{AC}\)
=>\(AB=10\cdot tan50\simeq11,92\left(cm\right)\)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{10^2+11.92^2}\simeq15,56\left(cm\right)\)
c: Xét ΔABC vuông tại A có \(cosB=\dfrac{3}{4}\)
=>\(\dfrac{AB}{BC}=\dfrac{3}{4}\)
=>\(\dfrac{5}{BC}=\dfrac{3}{4}\)
=>\(BC=\dfrac{20}{3}\)
Xét ΔABC vuông tại A có cosB=3/4
nên \(\widehat{B}\simeq41^0\)
=>\(\widehat{C}=49^0\)
\(AC=\sqrt{BC^2-AB^2}=\sqrt{\left(\dfrac{20}{3}\right)^2-5^2}=\dfrac{5\sqrt{7}}{3}\left(cm\right)\)
AD
15 tháng 10 2023
a, Theo định lý Pytago :
\(AB^2+AC^2=BC^2\\ \Rightarrow AB=\sqrt{20^2-16^2}=12\)
\(cosB=\dfrac{AB}{BC}=\dfrac{12}{20}\Rightarrow\widehat{B}=53^o8'\)
\(cosC=\dfrac{AC}{BC}=\dfrac{16}{20}\Rightarrow\widehat{C}=36^o52'\)
b, Vì tam giác ABC vuông tại A
\(\widehat{B}+\widehat{C}=90^o\\ \Rightarrow\widehat{B}=90^o-50^o=40^o\)
\(cosC=\dfrac{AC}{BC}\Rightarrow BC=\dfrac{AC}{cosC}=\dfrac{10}{cos50^o}\approx15,6\)
\(tanC=\dfrac{AB}{AC}\Rightarrow AB=tanC\times AC=tan50^o\times10\approx11,9\)
c,
\(cosB=\dfrac{AB}{BC}\\ \Rightarrow BC=\dfrac{AB}{cosB}=\dfrac{5}{\dfrac{3}{4}}=\dfrac{20}{3}\)
Theo định lý Pytago :
\(AB^2+AC^2=BC^2\\ \Rightarrow AC=\sqrt{\left(\dfrac{20}{3}\right)^2-5^2}=\dfrac{5\sqrt{7}}{3}\)
\(cosB=\dfrac{3}{4}\Rightarrow\widehat{B}=41^o25'\\ sinC=\dfrac{AB}{BC}=\dfrac{5}{\dfrac{20}{3}}=48^o35'\)
20 tháng 10 2023
a: Sửa đề: vẽ dây AD vuông góc với đường kính của (O) tại I
ΔABC vuông tại A
=>ΔABC nội tiếp đường tròn đường kính BC
=>BC là đường kính của (O)
mà AD vuông góc với đường kính của (O)
nên AD\(\perp\)BC tại I
=>B,I,C thẳng hàng
b: BC=2*OB=8cm
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ACB}=90^0-50^0=40^0\)
Xét ΔABC vuông tại A có \(sinACB=\dfrac{AB}{BC}\)
=>\(\dfrac{AB}{8}=sin40\)
=>\(AB\simeq5,14\left(cm\right)\)
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{8^2-5.14^2}\simeq6,13\left(cm\right)\)
c: ΔOAD cân tại O
mà OI là đường cao
nên I là trung điểm của AD
ΔABC vuông tại A có AI là đường cao
nên \(AI^2=IB\cdot IC\)
=>\(IB\cdot IC=IA\cdot ID\)
PT
1
CM
24 tháng 12 2019
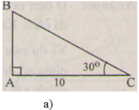
∠B = 90o - ∠C = 90o - 30o = 60o
c = b.tgC = 10.tg 30o ≈ 5,77 (cm)
PT
1
CM
27 tháng 12 2018
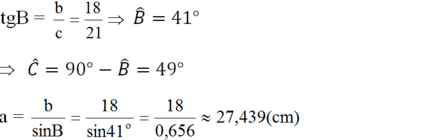
(Ghi chú: Bạn nên sử dụng các kí hiệu cạnh là a, b, c (thay vì BC, AC, AB) để đồng bộ với đề bài đã cho.
Cách để nhớ các cạnh là: cạnh nào thiếu chữ cái nào thì chữ cái đó là kí hiệu của cạnh đó. Ví dụ: cạnh AB thiếu chữ cái C nên c là kí hiệu của cạnh.
hoặc cạnh đối diện với góc nào thì đó chính là kí hiệu của cạnh. Ví dụ: cạnh đối diện với góc B là cạnh b (chính là cạnh AC))
∠B = 90o - ∠C = 90o - 35o = 55o
b = asinB = 20.sin35o ≈ 11,47 (cm)
c = asinC = 20.sin55o ≈ 16,38 (cm)