Có bao nhiêu số nguyên dương không lớn hơn 1000 chia hết cho 7 hoặc chia hết cho 11?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

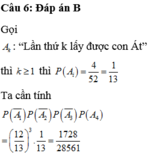

Đáp án C
Gọi A là tập các số nguyên dương không lớn hơn 1000 chia hết cho 7,
B là tập các số nguyên dương không lớn hơn 1000 chia hết cho 11,
Khi đó A ∩ B là tập các số nguyên không lớn hơn 1000 chia hết cho 7 và chia hết cho 11,
A ∪ B là tập các số nguyên không lớn hơn 1000 chia hết cho 7 hoặc chia hết cho 11.
Trong các số nguyên dương không lớn hơn 1000 ta có:
+) 1000 7 số nguyên dương chia hết cho 7.
+) 1000 11 số nguyên dương chia hết cho 11.
+) Vì 7 và 11 là hai số nguyên tố cùng nhau nên số nguyên chia hết cho 7 và 11 là số nguyên chia hết cho (7.11). Số các số này là 1000 7 .11 .
Do đó
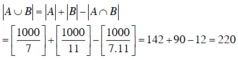

Đáp án C
Gọi A là tập các số nguyên dương không lớn hơn 1000 chia hết cho 7, B là tập các số nguyên dương không lớn hơn 1000 chia hết cho 11,
Khi đó A ∩ B là tập các số nguyên không lớn hơn 1000 chia hết cho 7 và chia hết cho 11, A ∪ B là tập các số nguyên không lớn hơn 1000 chia hết cho 7 hoặc chia hết cho 11.
Trong các số nguyên dương không lớn hơn 1000 ta có:

+) Vì 7 và 11 là hai số nguyên tố cùng nhau nên số nguyên chia hết cho 7 và 11 là số nguyên chia hết cho . Số các số này là ![]()
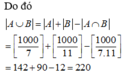

Số số nguyên dương chia hết cho 7 là: \(S_1=\dfrac{994-7}{7}+1=142\)
Số số vừa chia hết cho 7 vừa chia hết cho 5 (nghĩa là chia hết 35): \(S_2=\dfrac{980-35}{35}+1=28\)
Số số vừa chia hết cho 7 vừa chia hết cho 2: \(S_3=\dfrac{994-14}{14}+1=71\)
Số số chia hết cho cả 7;2;5 là: \(S_4=\dfrac{980-70}{70}+1=14\)
Số số thỏa mãn yêu cầu đề bài: \(S_1+S_4-\left(S_2+S_3\right)=57\)

Số chia hết cho 3 có dạng 3a ta có 0 < 3a ≤ 1000 ⇔ 0 < a < 333,3
Mà a nguyên nên có 333 số thỏa mãn
Số chia hết cho 5 có dạng 5b ta có 0 < 5b ≤ 1000 ⇔ 0 < b < 200
nên có 200 số thỏa mãn
Số chia hết cho cả 3 và 5 có dạng 15c ta có 0 < 15c ≤ 1000 ⇔ 0 < c < 66,6
nên có 66 số thỏa mãn
Do đó số các số thỏa mãn đề bài là 333 + 200 – 66 =467.
Chọn D.

Số chia hết cho 3 có dạng 3a ta có 0 < 3a ≤ 1000 ⇒ 0< a < 333,3 nên có 333 số thỏa mãn.
Số chia hết cho 5 có dạng 5b ta có 0 < 5b ≤ 1000 ⇒ 0< b < 200 nên có 200 số thỏa mãn.
Số chia hết cho cả 3 và 5 có dạng 15c ta có nên có 66 số thỏa mãn.
Do đó số các số thỏa mãn đề bài là 333 + 200 – 66 =467.
Chọn D.

a) Tập hợp các số chia hết cho 2 nhỏ hơn 1000 là { 0 ; 2 ; 4 ; ... ; 996 ; 998 }
Số các phần tử thuộc tập hợp trên là: ( 998 – 0 ) : 2 + 1 = 500 (phần tử)
b) Tập hợp các số chia hết cho 5 nhỏ hơn 1000 là { 0 ; 5 ; 10 ;... ; 990 ; 995 }
Số các phần tử thuộc tập hợp trên là: ( 995 – 0 ) : 5 + 1 = 200 (phần tử)
c) Trong một chục có 4 số chia hết cho 2 nhưng không chia hết cho 5.
Từ 0 đến 999 có 100 chục nên ta có: 4 . 100 = 400 (số)
Số 1000 không phải đếm.
Vậy cả 400 số chia hết cho 2 nhưng không chia hết cho 5.