Tìm các thừa số và tích của các phép nhân sau :
a) x y ¯ . x y x ¯ = x y x y ¯
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
22 tháng 12 2018
Đúng(0)
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
18 tháng 9 2018
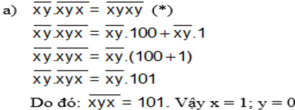
a/ \(x.y.xy=yyy=y.111\Rightarrow x.xy=111=3.37\Rightarrow x=3;y=7\)
\(\Rightarrow3.7.37=777\)
b/ \(xy.xyz=xyxy=xy.101\Rightarrow xyz=101\Rightarrow x=z=1;y=0\)
\(\Rightarrow10.101=1010\)
2 tháng 8 2015
a,(x+y)(2a-4)
b,(x+y)(a-b)
c,a(b+a)(x-5)
d,2a(a+2)(x+y)
**** cho mk nha
CW
7 tháng 7 2016
a) (x+y)(x+y) = x^2 + xy +xy + y^2 = x^2 + 2xy + y^2
b) (x-y)(x-y)= x^2 - xy - xy +y^2 = x^2 - 2xy + y^2
c) (x+y)(x-y)= x^2 + xy - xy - y^2 = x^2 - y^2
d) (x+5)(x-1)= x^2 + 5x - x -5 = x^2 + 4x -5
Q
8 tháng 9 2017
a) (x.y)+(x.y)
=> (x.x)+(y.y)
=> x2+y2
b) (x-y)(x-y)
=> (x.x)-(y.y)
=> x2-y2
c) (x+y)(x-y)
=> x2 - y2
d) (x+5).(x-1)
Áp dụng bài c . Ta có :
=> x(x-1) + 5(x-1)
=> x2 - x + 5x - 5
= x2 + 4x - 5
22 tháng 1 2020
1) A=(-125)(8x-8y)
A=(-125).8(x-y)
A=(-1000)(x-y)
Thay vào đó ta có :
A=(-1000).[(-43)-17]
A=(-1000).(-60)
A=60000
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
a) \(y = 2x(x - 3) = 2{x^2} - 6\)
Hàm số có lũy thừa bậc cao nhất của x là bậc hai
b) \(y = x({x^2} + 2) - 5 = {x^3} + 2x - 5\)
Hàm số có lũy thừa bậc cao nhất của x là bậc ba
c) \(y = - 5(x + 1)(x - 4) = - 5{x^2} + 15x + 20\)
Hàm số có lũy thừa bậc cao nhất của x là bậc hai
NV
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
28 tháng 3 2023
\(\overline{x,y}\) = \(y,x\) \(\times\) 3 + 1,3
10 \(\times\) \(\overline{x,y}\) = 10 \(\times\) ( \(\overline{y,x}\) \(\times\) 3 + 1,3)
\(\overline{xy}\) = \(\overline{yx}\) \(\times\) 3 + 13 => nếu \(x\) là chữ số lẻ thì y phải chẵn và ngược lại
\(\overline{yx}\) = ( \(\overline{xy}\) - 13) : 3
\(\overline{xy}\) ≤ 99 ⇒ \(\overline{yx}\) ≤ (99-13) : 3 = 28,66 ⇒ y =1; 2
Mặt khác ( \(\overline{xy}\) - 13 ) \(⋮\) 3 => \(x\) + \(y\) - 1 - 3 ⋮ 3 (1)
Thay \(y\) = 1 vào (1) ta có : \(x\) + 1 - 1 - 3 ⋮ 3
⇒ \(x\) ⋮ 3 ⇒ \(x\) = 3; 6; 9
vì y = 1 => \(x\) = 6 ( theo tính chẵn lẻ ở trên).
ta có : 6,1 = 1,6 \(\times\) 3 + 1,3 ( Đúng)
Thay y = 2 vào (1) ta có : \(x\) + 2 - 1 - 3 ⋮ 3 ⇒ \(x\) = 2; 5; 8
Vì y = 2 => \(x\) = 5 ( theo tính chẵn lẻ ở trên)
Ta có : 5,2 < 2,5 \(\times\) 3 + 1,3
=> y = 2; \(x=5\) loại
Vậy chữ số \(x\); \(y\) thỏa mãn đề bài là \(x\) = 6; y = 1
10 tháng 2 2019
1. Áp dụng bất đẳng thức \(\frac{1}{a}+\frac{1}{b}\ge\frac{4}{a+b}\) với \(a=x^3+3xy^2,b=y^3+3x^2y\) (a;b > 0)
(Bất đẳng thức này a;b > 0 mới dùng được)
\(A\ge\frac{4}{x^3+3xy^2+y^3+3x^2y}=\frac{4}{\left(x+y\right)^3}\ge\frac{4}{1^3}=4\)
Dấu "=" xảy ra khi: \(\hept{\begin{cases}x^3+3xy^2=y^3+3x^2y\\x+y=1\end{cases}\Leftrightarrow\hept{\begin{cases}x^3-3x^2y+3xy^2-y^3=0\\x+y=1\end{cases}}}\)
\(\Leftrightarrow\hept{\begin{cases}\left(x-y\right)^3=0\\x+y=1\end{cases}}\Leftrightarrow x=y=\frac{1}{2}\)
3 tháng 2 2021
a) Ta có: \(\dfrac{3+x}{7+y}=\dfrac{3}{7}\)
\(\Leftrightarrow\dfrac{x+3}{3}=\dfrac{y+7}{7}\)
mà x+y=20
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x+3}{3}=\dfrac{y+7}{7}=\dfrac{x+y+3+7}{3+7}=\dfrac{20+10}{10}=3\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x+3}{10}=3\\\dfrac{y+7}{7}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+3=30\\y+7=21\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=27\\y=14\end{matrix}\right.\)
Vậy: x=27; y=14