Có bao nhiêu cách xếp 7 người vào hai dãy ghế sao cho dãy ghế đầu có 4 người và dãy sau có 3 người.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
SG
1
18 tháng 5 2017
Chọn 4 người để xếp vào 4 ghế ở dãy đầu : có \(A_7^4\) cách. Còn lại 3 người xếp vào 3 ghế ở dãy sau : Có 3! cách
Vậy có tất cả \(A_7^4.3!=5040\) cách xếp
VT
16 tháng 1 2019
bài mẫu nè:
gọi số dãy ghế là x, số ghê là y
theo đb ta có hpt
(x-2)(y+2)=288
xy=288
giải pt tìm đk x=18; y=16
LL
26 tháng 5 2018
Gọi số dãy ghế ban đầu có trong phòng là x(dãy)
ĐK: x thuộc N*, x thuộc Ư(500)
Thì số ghế xếp mỗi dãy là : \(\frac{500}{x}\)(ghế)
Nếu thêm 3 dãy ghế và 1 dãy ghế thêm 2 chỗ thì được 616 người, nên ta có: \(\left(x+3\right).\left(\frac{500}{x}+2\right)=616\)
<=> 500 + 2x + \(\frac{1500}{x}\)+6 = 616
<=> -110 + 2x + \(\frac{1500}{x}\)=0
<=> 2x2 -110x + 1500 = 0
<=> x2 -55x + 750 = 0
Giải pt ta được:
x1 = 30
x2 = 25
.Khi x = x1 = 30, ta có số ghế của mỗi dãy: 500 : 30 =50/3 (KTMĐK)
.Khi x = x2 = 25, ta có số ghế của mỗi dãy: 500 : 25 =20 (TMĐK)
Vậy, ban đầu phòng học có 25 dãy ghế, mỗi dãy có 20 ghế.
AH
Akai Haruma
Giáo viên
19 tháng 12 2021
Lời giải:
Giả sử ban đầu có $a$ dãy ghế thì mỗi dãy có $b$ người. Trong đó $a,b$ là số tự nhiên $\neq 0$. Ta có: $ab=150(1)$
Khi thêm 71 người thì có tổng $150+71=221$ người.
Số dãy ghế: $a+2$
Số người mỗi dãy: $b+3$
Ta có: $(a+2)(b+3)=221(2)$
Từ $(1); (2)\Rightarrow 3a+2b=65$
$\Rightarrow b=\frac{65-3a}{2}$. Thay vào $(1)$ thì:
$a.\frac{65-3a}{2}=150$
$\Leftrightarrow a(65-3a)=300$
$\Leftrightarrow 3a^2-65a+300=0$
$\Leftrightarrow a=15$ (chọn) hoặc $a=\frac{20}{3}$ (loại)
Vậy có $15$ dãy ghế.
1 tháng 6 2015
Gọi số dãy là x, số người ngồi trong mỗi dãy là y dk:...
Theo bài ra ra có xy =70 (1)
Nếu ta bớt đi 2 dãy ghế thì mỗi dãy ghế còn lại phải xếp thêm 4 người ngồi mới đủ chỗ
=> (x-2)(y+4) = 70 (2)
Từ (1) và (2) ta có hệ phương trình...................
Giải ra được x = 7 ; y = 10
15 tháng 2 2018
Gọi số dãy ghế ban đầu là a [a>0 ,a thuộc N]
=>Số người trên mỗi dãy ghế là : \(\frac{70}{a}\)
Khi bớt đi 2 dãy ghế => Số dãy ghế còn lại là : a-2
Số người trên mỗi dãy ghế lúc đó là : \(\frac{70}{a-2}\)
Theo bài ra ta có : \(\frac{70}{a}+4=\frac{70}{a-2}\)
=> 70[a-2]+4a[a-2]=70a =>35[a-2]+2a[a-2]=35a
=> 35a-70+2a\(^2\)-4a=35a
=> 2a\(^2\)-4a-70=0
=> \(a^2-2a-35=0=>a^2-2a+1-36=0=>\left[a-1^2\right]=36=6^2\). Có 2 trường hợp
Trường hợp 1 : a-1 = -6 => a = - 5 [loại]
Trường hợp 2 : a - 1 = 6 => a = 7
Còn đây bạn làm nốt tiếp
Vậy phòng họp lúc đầu có 7 dãy ghế và 10 người
CM
23 tháng 10 2018
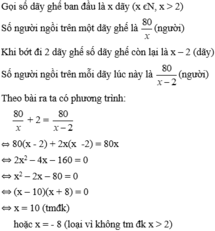
Vậy số dãy ghế ban đầu là 10 dãy và số người ngồi trên 1 dãy là 8 người.
VA
2 tháng 2 2019
Giả sử hội trường có a dãy và b là số ghế của mỗi dãy. (a,b∈N∗a,b∈N∗).
Ta có phương trình: ab=500ab=500 và
⇒(a−3)(b+3)=506⇒ab−3b+3a−9=506⇒3(a−b)=15⇒a−b=5⇒a(a−5)=500⇔a=25⇒(a−3)(b+3)=506⇒ab−3b+3a−9=506⇒3(a−b)=15⇒a−b=5⇒a(a−5)=500⇔a=25
Vậy lúc đầu người ta định xếp 2525 dãy ghế.
Chọn 4 người để xếp vào 4 ghế ở dãy đầu : Có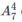
cách. Còn lại 3 người xếp vào 3 ghế ở dãy sau : có 3! cách.
Vậy có tất cả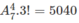
cách xếp.