Giải bất phương trình sau x2 - x - 6 ≤ 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
1
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 3 2022
\(f\left(x\right)=\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x^2-5x+6\right)\left(5-x\right)}>0\)
\(\Leftrightarrow\dfrac{\left(3x-4\right)\left(2x-3\right)}{\left(x-2\right)\left(x-3\right)\left(5-x\right)}>0\)
Bảng xét dấu:
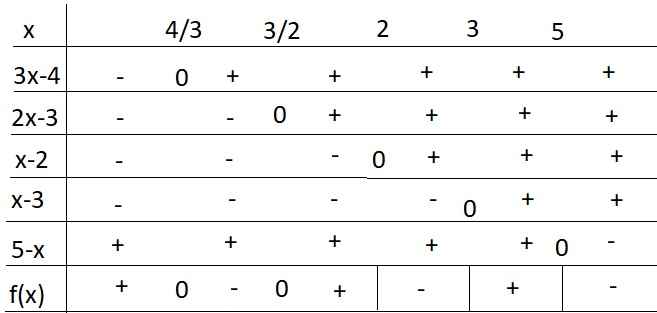
Từ bảng xét dấu ta thấy nghiệm của BPT là: \(\left[{}\begin{matrix}x< 5\\\dfrac{3}{2}< x< 2\\3< x< 5\end{matrix}\right.\)
PT
1
CM
10 tháng 8 2019
( x 2 / 3 ) + 3 x + 6 < 0 ⇔ x 2 + 9 x + 18 < 0 ⇔ -6 < x < -3
CM
17 tháng 7 2017
Chọn D
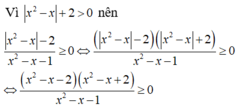
Bảng xét dấu
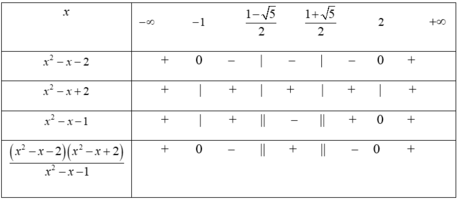
Dựa vào bảng xét dấu, ta có tập nghiệm của bất phương trình đã cho là
CM
17 tháng 8 2019
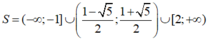
Chọn C
ĐKXĐ:
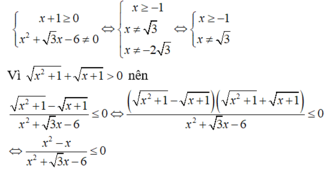
Bảng xét dấu
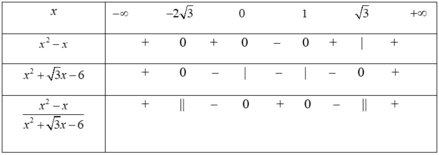
Dựa vào bảng xét dấu và đối chiếu điều kiện, ta có tập nghiệm của bất phương trình đã cho là
23 tháng 2 2022
Bài 1:
a: \(\Leftrightarrow x^2-5x+6< =0\)
=>(x-2)(x-3)<=0
=>2<=x<=3
b: \(\Leftrightarrow\left(x-6\right)^2< =0\)
=>x=6
c: \(\Leftrightarrow x^2-2x+1>=0\)
\(\Leftrightarrow\left(x-1\right)^2>=0\)
hay \(x\in R\)
BD
1
28 tháng 1 2022
\(\Leftrightarrow\left(x^4+5x^2+6\right)\left(x^4+5x^2+4\right)-24\)
Đặt \(x^4+5x^2+6=t\)
\(t\left(t-2\right)-24=t^2-2t-24\)
\(\Leftrightarrow t^2-2t+1-25=\left(t-1\right)^2-5^2=\left(t-6\right)\left(t+4\right)>0\)
TH1 : \(\left\{{}\begin{matrix}t-6>0\\t+4>0\end{matrix}\right.\Leftrightarrow t>6\)
TH2 : \(\left\{{}\begin{matrix}t-6< 0\\t+4< 0\end{matrix}\right.\)<=> t < -4
Theo cách đặt \(x^4+5x^2+6>6\Leftrightarrow x^2\left(x^2+5\right)>0\)* luôn đúng *
\(x^4+5x^2+6< -4\Leftrightarrow x^4+5x^2+10< 0\)
\(\Leftrightarrow x^4+\dfrac{2.5}{2}x^2+\dfrac{25}{4}+\dfrac{15}{4}< 0\Leftrightarrow\left(x^2+\dfrac{5}{2}\right)^2+\dfrac{15}{4}< 0\)( vô lí )
28 tháng 1 2022
Cậu làm thiếu rất nhiều bước và có thể người khác sẽ khó hiểu. Xem cách trình bày của mình nè.
NN
2
Y
11 tháng 4 2022
\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow x-1< 3\)
\(\Leftrightarrow x< 4\)
\(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(2+x\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2-x=0\\2+x=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\\x=-2\end{matrix}\right.\)
\(\dfrac{x+2}{x-5}< 0\)
\(\Leftrightarrow x+2< 0\)
\(\Leftrightarrow x< -2\)
11 tháng 4 2022
a)\(x^2-2x+1< 9\)
\(\Leftrightarrow\left(x-1\right)^2< 9\)
\(\Leftrightarrow\left(x-1\right)^2-9< 0\)
\(\Leftrightarrow\left(x-1-3\right)\left(x-1+3\right)< 0\)
\(\Leftrightarrow\left(x-4\right)\left(x+2\right)< 0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4< 0\\x+2>0\end{matrix}\right.hay\left[{}\begin{matrix}x-4>0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 4\\x>-2\end{matrix}\right.hay\left[{}\begin{matrix}x>4\\x< -2\end{matrix}\right.\)(vô lý)
-Vậy nghiệm của BĐT là \(-2< x< 4\).
b) \(\left(x-1\right)\left(4-x^2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(2-x\right)\left(x+2\right)\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(x-2\right)\left(x+2\right)\le0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1< 0\\x-2>0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2< 0\\x+2>0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1>0\\x-2 >0\\x+2< 0\end{matrix}\right.\) hay \(\left[{}\begin{matrix}x-1< 0\\x-2< 0\\x+2< 0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x< 1\\x>2\\x>-2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x>1\\x< 2\\x>-2\end{matrix}\right.\) (có thể xảy ra) hay
\(\left[{}\begin{matrix}x>1\\x>2\\x< -2\end{matrix}\right.\) (vô lí) hay \(\left[{}\begin{matrix}x< 1\\x< 2\\x< -2\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(x< -2\) hay \(1< x< 2\).
c) ĐKXĐ: \(x\ne5\)
\(\dfrac{x+2}{x-5}< 0\Leftrightarrow\left[{}\begin{matrix}x+2< 0\\x-5>0\end{matrix}\right.hay\left[{}\begin{matrix}x+2>0\\x-5< 0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x< -2\\x>5\end{matrix}\right.\)(vô lí) hay
\(\left[{}\begin{matrix}x>-2\\x< 5\end{matrix}\right.\) (có thể xảy ra)
-Vậy nghiệm của BĐT là \(-2< x< 5\)
PT
1
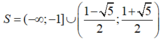
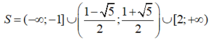
x2 - x - 6 ≤ 0
Xét tam thức f(x) = x2 - x - 6 có hai nghiệm x = -2 và x = 3, hệ số a = 1 > 0
Do đó f(x) ≤ 0 khi -2 ≤ x ≤ 3.
Vậy tập nghiệm của bất phương trình là: T = [-2; 3]