Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án D
Xét hàm số y = x 3 + x 2 + m x - 1 có y ' = 3 x 2 + 2 x + m , ∀ x ∈ ℝ
Để hàm số có 2 điểm cực trị ⇔ y ' = 0 có 2 nghiệm phân biệt ⇔ 1 - 3 m > 0 ⇔ m < 1 3
Gọi x 1 , x 2 lần lượt là các điểm cực tiểu và cực đại của hàm số đã cho
Theo Viet, ta có x 1 + x 2 = - 2 3 x 1 x 2 = m 3 mà x 1 > 0 suy ra x 1 x 2 = m 3 < 0 ⇔ m < 0
Kết hợp m ∈ - 5 ; 6 mà m ∈ ℤ → m = - 4 ; - 3 ; - 2 ; - 1
Chọn A.
Đồ thị hàm số có điểm cực tiểu khi và chỉ khi phương trình y’ = 0 có hai nghiệm phân biệt
Khi đó, giả sử x1, x2 là hai nghiệm của phương trình y’=0.
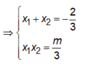
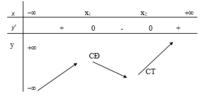
Bảng biến thiên
Do 
nên hoặc nên điểm cực tiểu của đồ thị hàm số 
nằm bên phải trục tung 
(1),(2) => m < 0
Đáp án C
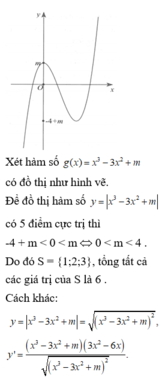
Đồ thị hàm số đã cho có 5 điểm cực trị khi và chỉ khi phương trình y’ = 0 có 5 nghiệm phân biệt và y’ đổi dấu qua 5 nghiệm đó, điều này tương đương với x 3 - 3 x 2 + m có ba nghiệm phân biệt khác 0 và 2
Ta có đạo hàm y’ = 3x2+ 2x+ m.
Hàm số có cực trị khi ∆ ' = 1 - 3 m > 0 ⇔ m < 1 3
Do hàm số có a=1>0 ⇒ x C T > x C D
Yêu cầu bài toán trở thành phương trình y’ = 0 có ít nhất 1 nghiệm dương
Do x 1 + x 2 = - 2 3 < 0 x 1 x 2 = m 3 ⇒ m < 0 là giá trị cần tìm.
Vậy - 5 ; 6 ∩ S = ( - 5 ; 0 )
Mà m nguyên nên chọn -4; -3; -2; -1. Có 4 giá trị thỏa mãn.
Chọn D.