Cho t//z và {c cắt t tại a
c cắt z tại b
Chỉ ra các cặp góc bằng nhau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ Xét tg BIC có
\(\widehat{BIC}=180^o-\left(\widehat{IBC}+\widehat{ICB}\right)=180^o-\dfrac{\widehat{B}}{2}-\dfrac{\widehat{C}}{2}=\)
\(=180^o-\left(\dfrac{\widehat{B}+\widehat{C}}{2}\right)=180^o-\left[\dfrac{180^o-\widehat{A}}{2}\right]=90^o+\dfrac{\widehat{A}}{2}\left(dpcm\right)\)
b/ Để c/m câu này ta chứng minh bài toán phụ: " Hai đường phân giác ngoài của 2 góc với đường phân giác trong của góc còn lại đồng quy"
Có hai đường phân giác của các góc ngoài của góc B và góc C cắt nhau tại J.
Từ J dựng các đường vuông góc với AB; AC; BC cắt 3 cạnh trên lần lượt tại D; E; F
Vì J thuộc đường phân giác của \(\widehat{DBC}\) nên JD=JF
Vì J thuộc đường phân giác của \(\widehat{ECB}\) nên JE=JF
(Mọi điểm thuộc đường phân giác của một góc thì cách đều hai cạnh của góc)
=> JD=JE
Xét tg vuông ADJ và tg vuông AEJ có
ẠJ chung; JD=JE (cmt) => tg ADJ = tg AEJ (hai tg vuông có cạnh huyền và cạnh góc vuông tương ứng bằng nhau)
\(\Rightarrow\widehat{DAJ}=\widehat{EAJ}\) => Ạ là phân giác của góc \(\widehat{BAC}\)
Áp dụng vào bài toán:
Nối AJ => AJ là phân giác của \(\widehat{BAC}\) => AJ phải đi qua I (Trong tg 3 đường phân giác trong đồng quy) => A; I; J thẳng hàng
c/ Vì J; H; K bình đẳng nên B; I; K thẳng hàng và C; I; H thẳng hàng
=> AJ; BK; CH đồng quy tại I

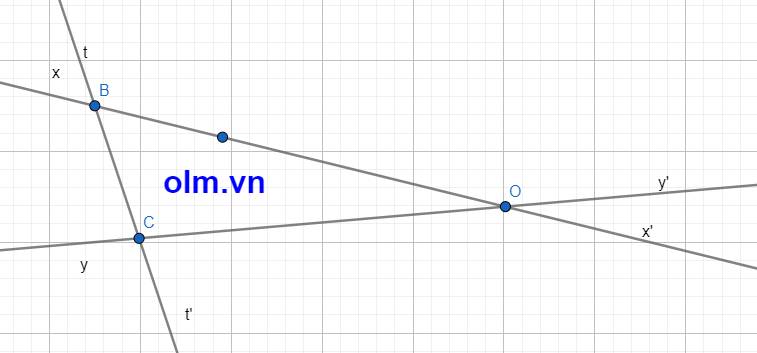
Các cặp so le trong là: góc CBO và góc BCy
góc xBC và góc BCO
Các cặp góc đồng vị là: góc tBO và góc t'CO
góc tBx và góc yCt'

Các cặp so le trong là: góc CBO và góc BCy
góc xBC và góc BCO
Các cặp góc đồng vị là: góc tBO và góc t'CO
góc tBx và góc yCt'

a) Ta có: EF//BC(gt) =>\(\left\{{}\begin{matrix}\text{^EOB = ^OBC (SLT)}\\\text{ ^FOC = ^OCB (SLT)}\\\text{^AEF = ^B (Đồng vị)}\\\text{^AFE = ^C (Đồng vị)}\end{matrix}\right.\)
Có: ^OBC = ^OBA ( BF là phân giác ^B)
mà: ^EOB = ^OBC (cmt)
=> ^EOB = ^OBA => tam giác EBO cân tại E
Có: ^OCA = ^OCB ( BF là phân giác ^B)
mà: ^FOC = ^OCB (cmt)
=> ^FOC = ^OCA => tam giác FCO cân tại E
Ta có: ^AEF = ^B (cmt)
^AFE = ^C (cmt)
Mà ^B = ^C (tam giác ABC cân tại A)
=> ^AEF = ^AFE => tam giác AEF cân tại A
Có : ^ABF = ^CBF = \(\dfrac{1}{2}\) ^B ( BF là phân giác ^B)
^ACE = ^BCE = \(\dfrac{1}{2}\) ^B ( CF là phân giác ^C)
mà : ^B = ^C (tam giác ABC cân tại A)
=> ^ACE = ^ABF = ^CBF = ^BCE
Xét tg OBC có: ^OBC = ^OCB (^CBF = ^BCE) => tg OBC cân tại O
Xét tam giác FCO và tam giác EBO có:
^FOC = ^FOB ( đối đỉnh)
^FCO = ^EBO (^ABF = ^ACE)
OB = OC ( tg OBC cân tại O )
=> tam giác FCO = tam giác EBO(g-c-g)