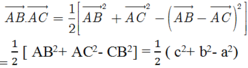Cho tam giác có AB=c, BC = a , CA=b ; ma , mb , mc là độ dài trung tuyến vẽ từ A, B, C . Cmr : \(\left(a^2+b^2+c^2\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\ge2\sqrt{3}\left(m_a+m_b+m_c\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
2
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 1 2022
Ta cần chứng minh:
\(\left(ab+bc+ca\right)^2\ge48\left(\dfrac{a+b+c}{2}\right)\left(\dfrac{a+b-c}{2}\right)\left(\dfrac{b+c-a}{2}\right)\left(\dfrac{c+a-b}{2}\right)\)
\(\Leftrightarrow\left(ab+bc+ca\right)^2\ge3\left(a+b+c\right)\left(a+b-c\right)\left(a+c-b\right)\left(b+c-a\right)\)
Mặt khác do a;b;c là 3 cạnh của 1 tam giác:
\(\Rightarrow\left(a+b-c\right)\left(a+c-b\right)\left(b+c-a\right)\le abc\)
Nên ta chỉ cần chứng minh:
\(\left(ab+bc+ca\right)^2\ge3abc\left(a+b+c\right)\) (đúng)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Ta có: \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right)\)
Mà \(\left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \widehat {BAC}\)\( \Rightarrow \cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = \cos \widehat {BAC}\)
Lại có: \(\cos \widehat {BAC} = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\)(suy ra từ định lí cosin)
\(\begin{array}{l} \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = AB.AC.\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\ \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AC} = c.b.\frac{{{b^2} + {c^2} - {a^2}}}{{2bc}}\\ \Leftrightarrow \overrightarrow {AB} .\overrightarrow {AC} = \frac{{{b^2} + {c^2} - {a^2}}}{2}\end{array}\)
N
13 tháng 2 2017
dùng Pitago đảo thử từng cặp 1 thôi:v
ta có: \(\left(b-c\right)^2+h^2=b^2+c^2-2bc+h^2\)(1)
vì tam giác ABC vuông ở A có đường cao AH nên \(a^2=b^2+c^2\)và\(AB.AB=AH.BC=2S\)hay\(b.c=a.h\)
\(\Rightarrow b^2+c^2-2bc+h^2=a^2-2ah+h^2=\left(a-h\right)^2\)