Question

[Mai Duy Khánh]

Cho tam giác ABC có diện tích 516 cm². Trên cạnh BC lấy 2 điểm P, Q sao cho PB = PQ = QC. Từ P kẻ đường thẳng song song AC, từ Q kẻ đường thẳng song song AB, 2 đường thẳng này cắt nhau tại M. 

a. So sánh diện tích tam giác AMC và APC.

b. Tính diện tích tam giác AMC.

c. Tính \(\frac{S_{BCM}}{S_{AMC}}\)

Answer 1

[Nguyễn Ngọc Anh Minh]

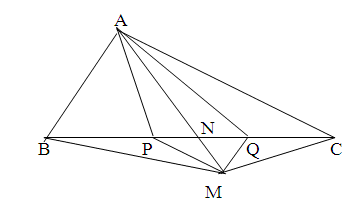
a/ Do MP//AC nên Đường cao hạ từ P xuống AC = đường cao hạ từ P xuống AC

Xét tg AMC và tg APC có AC chung nên

S(AMC) / S(APC) = Đường cao hạ từ P xuống AC / đường cao hạ từ P xuống AC = 1 

=> S(AMC) = S(APC)

b/ Xét tg APC và tg ABC có chung đường cao hạ từ A xuống BC nên

\(\frac{S_{APC}}{S_{ABC}}=\frac{PC}{BC}=\frac{2}{3}\Rightarrow S_{APC}=S_{AMC}=\frac{2xS_{ABC}}{3}=\frac{2x516}{3}=344cm^2\)