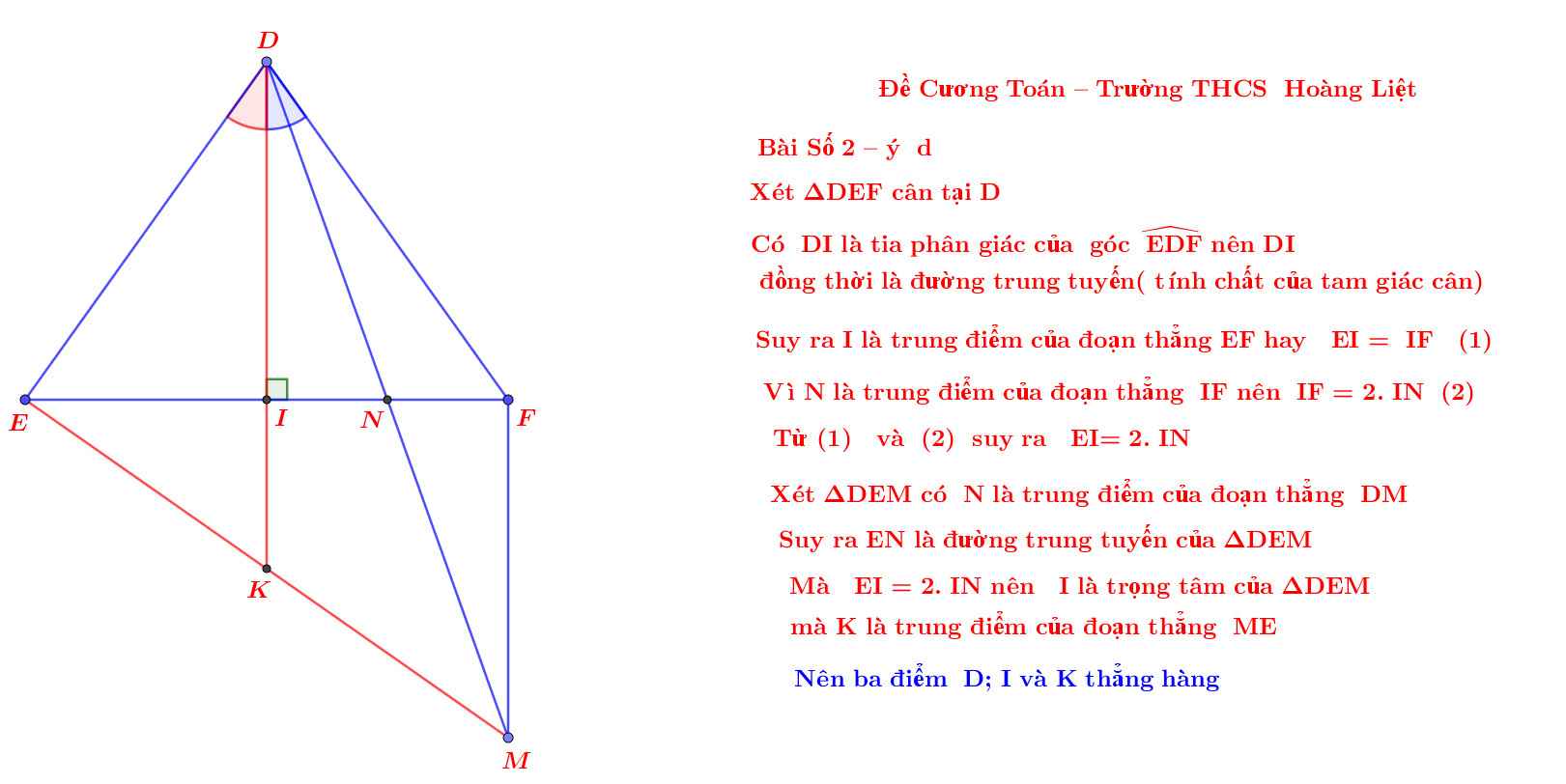
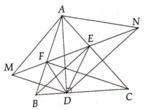
Cho tam giác DEF cân tại D, đường phân fiasco DI. Gọi N là trung điểm của IF. Vẽ điểm M sao cho N là trung điểm của DM. Chứng minh rằng:
a) Tam giác DIN=tam giác MNF; MF vuông góc EF.
b) DF>MF.
c) Góc IDN>góc NDF.
d) D,I,K thẳng hàng( K là trung điểm của ME)



a) Xét ΔDIN và ΔMNF có
DN=MN(N là trung điểm của DM)
\(\widehat{DNI}=\widehat{MNF}\)(hai góc đối đỉnh)
IN=NF(N là trung điểm của IF)
Do đó: ΔDIN=ΔMNF(c-g-c)
⇒\(\widehat{IDN}=\widehat{NMF}\)(hai góc tương ứng)
mà \(\widehat{IDN}\) và \(\widehat{NMF}\) là hai góc ở vị trí so le trong
nên DI//MF(dấu hiệu nhận biết hai đường thẳng song song)
Xét ΔEDI và ΔFDI có
DE=DF(ΔDEF cân tại D)
\(\widehat{EDI}=\widehat{FDI}\)(DI là tia phân giác của \(\widehat{EDF}\))
DI chung
Do đó: ΔEDI=ΔFDI(c-g-c)
⇒\(\widehat{DIE}=\widehat{DIF}\)(hai góc tương ứng)
mà \(\widehat{DIE}+\widehat{DIF}=180^0\)(hai góc kề bù)
nên \(\widehat{DIE}=\widehat{DIF}=\frac{180^0}{2}=90^0\)
⇒DI⊥EF
Ta có: DI⊥EF(cmt)
DI//FM(cmt)
Do đó: FM⊥EF(định lí 2 từ vuông góc tới song song)
b) Xét ΔIFM vuông tại F có IM là cạnh huyền
nên IM là cạnh lớn nhất trong ΔIFM(trong tam giác vuông, cạnh huyền là cạnh lớn nhất)
⇒IM>FM(1)
Xét ΔINM và ΔFND có
IN=FN(N là trung điểm của IF)
\(\widehat{INM}=\widehat{FND}\)(hai góc đối đỉnh)
NM=ND(N là trung điểm của MD)
Do đó: ΔINM=ΔFND(c-g-c)
⇒IM=FD(hai cạnh tương ứng)(2)
Từ (1) và (2) suy ra DF>MF(đpcm)
c) Xét ΔDFM có DF>MF(cmt)
mà góc đối diện với cạnh DF là \(\widehat{DMF}\)
và góc đối diện với cạnh MF là \(\widehat{FDM}\)
nên \(\widehat{DMF}>\widehat{FDM}\)(định lí 1 về quan hệ giữa cạnh và góc đối diện trong tam giác)
mà \(\widehat{DMF}=\widehat{IDN}\)(cmt)
nên \(\widehat{IDN}>\widehat{MDF}\)
hay \(\widehat{IDN}>\widehat{NDF}\)(đpcm)
d) Ta có: ΔEFM vuông tại F(EF⊥FM)
mà FK là đường trung tuyến ứng với cạnh huyền EM(K là trung điểm của EM)
nên \(FK=\frac{EM}{2}\)(định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
mà \(EK=\frac{EM}{2}\)(K là trung điểm của EM)
nên FK=EK
⇔K nằm trên đường trung trực của FE(tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: DE=DF(ΔDEF cân tại D)
nên D nằm trên đường trung trực của FE(tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: IE=IF(ΔEDI=ΔFDI)
nên I nằm trên đường trung trực của FE(tính chất đường trung trực của một đoạn thẳng)(5)
Từ (3), (4) và (5) suy ra D,I,K thẳng hàng(đpcm)