Cho tanα+cotα=m .Hãy tính giá trị của biểu thức tan\(^{ }\)3α+cot3α theo m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


tan 3 α + c o t 3 α = ( tan α + c o t α ) ( tan 2 α - tan α c o t α + c o t 2 α ) = m ( m 2 - 3 )

Ta có tanα + cotα = tanα + 1/tanα.
Do đó tanα + cotα ≤ -2 hoặc tanα + cotα ≥ 2.
Dấu “=” xảy ra khi tanα = cotα = -1 hoặc tanα = cotα = 1.
Với giả thiết tanα + cotα = -2 thì tanα = cotα = -1.
Do đó N = tan 3 α + c o t 3 α = -2
Đáp án là C.

Cách 1: \(\tan^2\alpha+\cot^2\alpha=\left(\tan\alpha+\cot\alpha\right)^2-2\tan\alpha\cot\alpha\) \(=2^2-2=2\)
\(\tan^3\alpha+\cot^3\alpha=\left(\tan\alpha+\cot\alpha\right)^3-3\tan\alpha\cot\alpha\left(\tan\alpha+\cot\alpha\right)\) \(=2^3-3.1.2=2\)
Cách 2: Ta thấy \(\cot\alpha=\dfrac{1}{\tan\alpha}\) nên ta có \(\tan\alpha+\dfrac{1}{\tan\alpha}=2\) (*). Áp dụng BDT AM-GM, ta có \(\tan\alpha+\dfrac{1}{\tan\alpha}\ge2\sqrt{\tan\alpha.\dfrac{1}{\tan\alpha}}=2\), do đó (*) xảy ra khi và chỉ khi \(\tan\alpha=\dfrac{1}{\tan\alpha}\Leftrightarrow\tan^2\alpha=1\Leftrightarrow\tan\alpha=1\) \(\Rightarrow\cot\alpha=1\). Từ đó dễ dàng tính được \(\tan^2\alpha+\cot^2\alpha=\tan^3\alpha+\cot^3\alpha=2\).
(Tuyệt đối không được dùng cách 2 khi \(\tan\alpha\) hoặc \(\cot\alpha\) âm nhé, vì bất đẳng thức AM-GM chỉ dùng cho số dương thôi.)



Chọn B.
Ta có P = tan3α + cot3α = (tanα + cotα) 3 - 3tanα.cotα( tanα + cotα)
= 53 - 3.5 = 110

tan 3 α + c o t 3 α = tan α + c o t α . tan 2 α - tan α . c o t α + c o t 2 α = 4 . tan α + c o t α 2 - 3 tan α . c o t α = 4 . 4 2 - 3 . 1 = 52
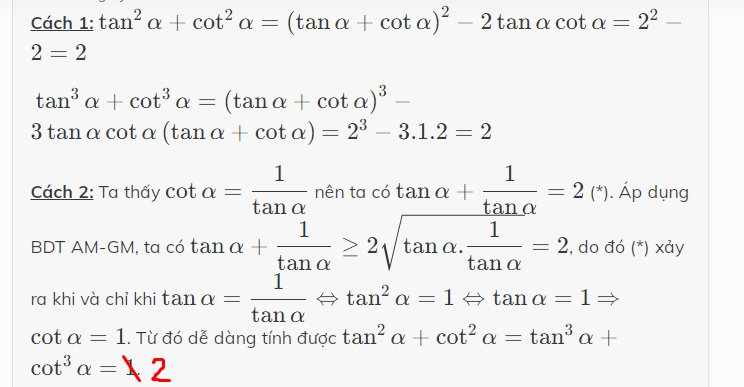
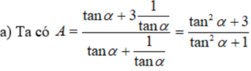
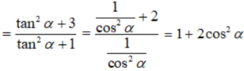
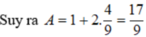

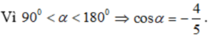
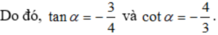
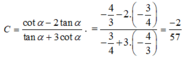
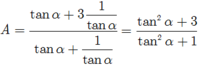
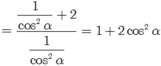
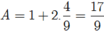
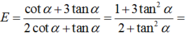

\(tan^3a+cot^3a=\left(tana+cota\right)^3-3tana.cota\left(tana+cota\right)\)
\(=m^3-3.1.m=m^3-3m\)