Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tan 3 α + c o t 3 α = ( tan α + c o t α ) ( tan 2 α - tan α c o t α + c o t 2 α ) = m ( m 2 - 3 )

Ta có tanα + cotα = tanα + 1/tanα.
Do đó tanα + cotα ≤ -2 hoặc tanα + cotα ≥ 2.
Dấu “=” xảy ra khi tanα = cotα = -1 hoặc tanα = cotα = 1.
Với giả thiết tanα + cotα = -2 thì tanα = cotα = -1.
Do đó N = tan 3 α + c o t 3 α = -2
Đáp án là C.

Chọn B.
Ta có P = tan3α + cot3α = (tanα + cotα) 3 - 3tanα.cotα( tanα + cotα)
= 53 - 3.5 = 110

tan 3 α + c o t 3 α = tan α + c o t α . tan 2 α - tan α . c o t α + c o t 2 α = 4 . tan α + c o t α 2 - 3 tan α . c o t α = 4 . 4 2 - 3 . 1 = 52

tan 2 α + c o t 2 α = ( tan α + c o t α ) 2 - 2 tan α c o t α = m 2 - 2

Trên đường tròn lượng giác,từ A(1,0) vẽ tiếp tuyến t’At với đường tròn lượng giác.
Từ B(0,1) vẽ tiếp tuyến s’Bs với đường tròn lượng giác .
Cho cung lượng giác AM có số đo α (α ≠ π/2 + kπ ). Gọi T là giao điểm của OM với trục t’At.
Gọi S là giao điểm của OM và trục s’Bs.
Khi β = α + kπ thì điểm cuối của góc β sẽ trùng với điểm T trên trục tan. Do đó
tan(α + kπ) = tanα.
Khi β = α + kπ thì điểm cuối của góc β sẽ trùng với điểm S trên trục cot. Do đó
cot(α + kπ) = cotα.

Vì \(\dfrac{\pi}{2}< \alpha< \pi\) \(\Rightarrow\) cos \(\alpha\) < 0
\(\Rightarrow\) cos \(\alpha\) = \(-\sqrt{1-sin^2\alpha}\) = \(-\dfrac{2\sqrt{2}}{3}\)
\(\Rightarrow\) tan \(\alpha\) = \(\dfrac{sin\alpha}{cos\alpha}=\dfrac{-\sqrt{2}}{4}\)
\(\Rightarrow\) cot \(\alpha\) = \(\dfrac{1}{tan\alpha}\) = \(-2\sqrt{2}\)
Chúc bn học tốt!
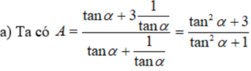
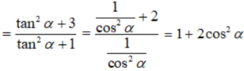
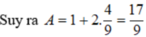

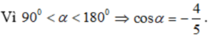
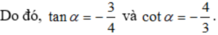
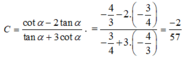
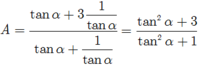
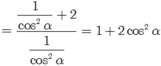
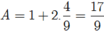

\(tan^3a+cot^3a=\left(tana+cota\right)^3-3tana.cota\left(tana+cota\right)\)
\(=m^3-3.1.m=m^3-3m\)