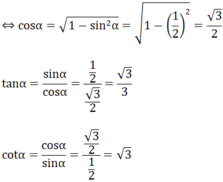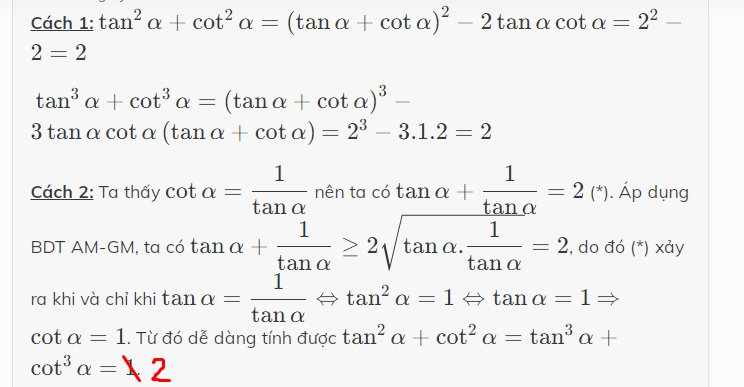TQ
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TQ
0
3 tháng 7 2023
Cách 1: \(\tan^2\alpha+\cot^2\alpha=\left(\tan\alpha+\cot\alpha\right)^2-2\tan\alpha\cot\alpha\) \(=2^2-2=2\)
\(\tan^3\alpha+\cot^3\alpha=\left(\tan\alpha+\cot\alpha\right)^3-3\tan\alpha\cot\alpha\left(\tan\alpha+\cot\alpha\right)\) \(=2^3-3.1.2=2\)
Cách 2: Ta thấy \(\cot\alpha=\dfrac{1}{\tan\alpha}\) nên ta có \(\tan\alpha+\dfrac{1}{\tan\alpha}=2\) (*). Áp dụng BDT AM-GM, ta có \(\tan\alpha+\dfrac{1}{\tan\alpha}\ge2\sqrt{\tan\alpha.\dfrac{1}{\tan\alpha}}=2\), do đó (*) xảy ra khi và chỉ khi \(\tan\alpha=\dfrac{1}{\tan\alpha}\Leftrightarrow\tan^2\alpha=1\Leftrightarrow\tan\alpha=1\) \(\Rightarrow\cot\alpha=1\). Từ đó dễ dàng tính được \(\tan^2\alpha+\cot^2\alpha=\tan^3\alpha+\cot^3\alpha=2\).
(Tuyệt đối không được dùng cách 2 khi \(\tan\alpha\) hoặc \(\cot\alpha\) âm nhé, vì bất đẳng thức AM-GM chỉ dùng cho số dương thôi.)
CM
3 tháng 6 2018
a, Ta có: cot 24 0 = tan 66 0 ; cot 57 0 = tan 33 0 ; cot 30 0 = tan 60 0
=> tan 16 0 < tan 33 0 < tan 60 0 < tan 66 0 < tan 80 0
=> tan 16 0 < cot 57 0 < cot 30 0 < cot 24 0 < tan 80 0
b, Ta có: cos 2 α = 1 - sin 2 α => cosα = 2 6 5 , tanα = sin α cos α = 6 12 và cotα = cos α sin α = 2 6
CM
28 tháng 9 2018
a, Tìm được sinα = 24 5 , tanα = 24 , cotα = 1 24
b, cosα = 5 3 , tanα = 2 5 , cotα = 5 2
c, sinα = ± 2 5 , cosα = ± 1 5 , cotα = 1 2
d, sinα = ± 1 10 , cosα = ± 3 10 , tanα = 1 3
5 tháng 2 2022
Đặt \(\tan\alpha=a;\cot\alpha=b\)
Theo đề, ta có: \(\left(a+b\right)^2-\left(a-b\right)^2\)
\(=a^2+2ab+b^2-a^2+2ab-b^2\)
\(=4ab=4\cdot\tan\alpha\cdot\cot\alpha=4\)
H9
HT.Phong (9A5)
CTVHS
24 tháng 8 2023
Ta có:
\(cot\alpha\cdot tan\alpha=1\)
\(\Rightarrow cot\alpha=\dfrac{1}{tan\alpha}\)
\(\Rightarrow cota=\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3}\)
Mà:
\(cot^2\alpha+1=\dfrac{1}{sin^2\alpha}\)
\(\Rightarrow sin\alpha=\sqrt{\dfrac{1}{cot^2\alpha+1}}\)
\(\Rightarrow sin\alpha=\sqrt{\dfrac{1}{\left(\dfrac{4}{3}\right)^2+1}}=\dfrac{3}{5}\)
Lại có:
\(cos^2\alpha+sin^2\alpha=1\)
\(\Rightarrow cos\alpha=\sqrt{1-sin^2a}\)
\(\Rightarrow cos\alpha=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)
GH
24 tháng 8 2023
\(tan\alpha=\dfrac{3}{4}\\ \Rightarrow cot\alpha=1:\dfrac{3}{4}=\dfrac{4}{3}\)
Có:
\(1+cot^2\alpha=\dfrac{1}{sin^2\alpha}\\ \Rightarrow sin\alpha=\sqrt{1:\left(1+\left(\dfrac{4}{3}\right)^2\right)}=\dfrac{3}{5}\)
\(\Rightarrow cos\alpha=\sqrt{1-\left(\dfrac{3}{5}\right)^2}=\dfrac{4}{5}\)
CM
23 tháng 7 2017
Cho α là góc nhọn, sinα = 1/2. Tính cosα; tanα; cotα
Ta có: sin 2 α + cos 2 α = 1
