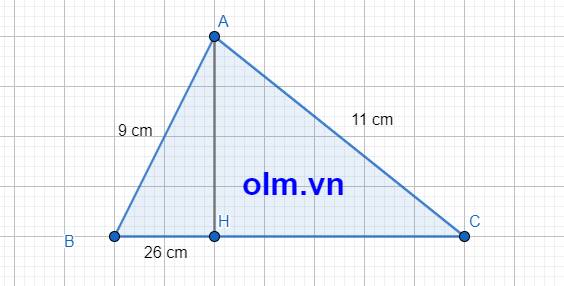
cho tam giác ABC có ab=9cm AC=11cm kẻ đường cao Ah Biết BH=26cm. tính Ch
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đề thế này thì tính ra âm à , cạnh góc vuông sao lơn hơn cạnh huyền trời ............
~ xem lại đề nha
~ học tốt!~

Ta có :
\(AH^2=AB^2+BH^2\left(1\right)\) (Δ ABH vuông tại H)
\(AH^2=AC^2+CH^2\left(2\right)\) (Δ ACH vuông tại H)
\(\left(1\right),\left(2\right)\Rightarrow AB^2+BH^2=AC^2+CH^2\)
\(\Rightarrow CH^2=AB^2+BH^2-AC^2\)
\(\Rightarrow CH^2=81+676-121=636\)
\(\Rightarrow CH=\sqrt[]{636}=\sqrt[]{4.159}=2\sqrt[]{159}\left(cm\right)\)
Vì AH là đường cao của tam giác ABC nên AH \(\perp\) BC \(\equiv\) H
⇒ \(\Delta\) AHB \(\perp\) \(\equiv\) H \(\Rightarrow\) AB > BH ⇒ 9 cm > 26 cm vô lý
Em có hai sựa lựa chọn: 1 là em chỉ ra cái sai của cô
2 là em xem lại đề bài của em

`Answer:`
Sửa lại đề: `BH=6cm`
Xét `triangleAHB` vuông tại `H` nên ta áp dụng định lý Pytago:
`BH^2+AH^2=AB^2`
`=>6^2+AH^2=9^2`
`=>AH^2=9^2-6^2=45`
`=>AH=\sqrt{45}cm`
Xét `triangleAHC` vuông tại `H` nên ta áp dụng định lý Pytago:
`AH^2+HC^2=AC^2`
`=>CH^2=AC^2-AH^2`
`=>CH^2=11^2-45=76`
`=>CH=\sqrt{76}cm`

d)
+ Xét \(\Delta ABD\) vuông tại \(D\left(gt\right)\) có:
\(AB^2=AD^2+BD^2\) (định lí Py - ta - go).
=> \(17^2=AD^2+15^2\)
=> \(AD^2=17^2-15^2\)
=> \(AD^2=289-225\)
=> \(AD^2=64\)
=> \(AD=8\left(cm\right)\) (vì \(AD>0\)).
+ Ta có: \(AD+CD=AC.\)
=> \(8+CD=17\)
=> \(CD=17-8\)
=> \(CD=9\left(cm\right).\)
+ Xét \(\Delta BDC\) vuông tại \(D\left(gt\right)\) có:
\(BC^2=BD^2+CD^2\) (định lí Py - ta - go).
=> \(BC^2=15^2+9^2\)
=> \(BC^2=225+81\)
=> \(BC^2=306\)
=> \(BC=\sqrt{306}\)
=> \(BC=3\sqrt{34}\left(cm\right)\) (vì \(BC>0\)).
Vậy \(BC=3\sqrt{34}\left(cm\right).\)
Chúc bạn học tốt!
Đề bài này sai rồi nhé
H B C A 9cm 12cm 6cm
Áp dụng đl pitago cho tg BAH vuông tại H có :
BH^2 + AH^2 = AB^2
<=> AH^2 = AB^2 - BH^2 = 9^2 - 6^2
<=> AH^2 = 81 - 36 = 45
<=> AH = \(\sqrt{45}\)
Áp dụng đl pitago cho tam giác ACH vuông tại H có :
AC^2 = AH^2 + CH^2
<=> CH^2 = AC^2 - AH^2
<=> CH^2 = 12^2 - \(\sqrt{45}\) ^2
<=> CH^2 = 144 - 45 = 99
<=> CH = \(\sqrt{99}\)
Vậy ...