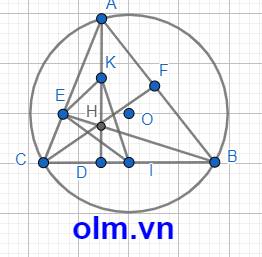
Cho đuờng tròn (O,R) có dây BC cố định, điểm A di chuyển trên cung lớn BC. Gọi AD, BE, CF là các đuờng cao và H là trực tâm của tam giác ABC, I là trung điểm của BC.
1) Chứng minh 4 điểm A,F,H,E cùng nằm trên một đuờng tròn và 4 điểm B,C,E,F cũng nằm trên một đuờng tròn
2) Khi cung nhỏ BC có số đo bằng 90*, tính độ dài dây cung BC và diện tích tam giác OBC
3) Đuờng thẳng qua E và vuông góc với EI cắt BC tại P.Chứng minh: PE^2=PB.PC