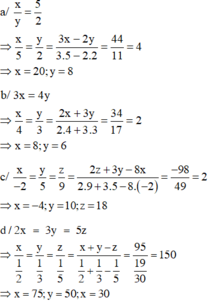Bài 1: Tìm x, y, z biết:
a. \(8x=3y\); \(5y=6z\) và \(2x+y-z=-34\)
b. \(6^{x+1}-200\cdot6^{x-1}=360\) \(\left(x\in N,x\ge2\right)\)
c. \(3^x+4^x=5^x\left(x\in N\right)\)
d. \(\frac{x-5}{7}=\frac{2y+3}{5}=z+19\) và \(x+y=z\)
e. \(\frac{x^3+y^3}{6}=\frac{x^3-2y^3}{4}\) và \(x^6\cdot y^6=64\)
g. \(\left(x^3-5\right)\left(x^3-10\right)\left(x^3-30\right)< 0\left(x\in Z\right)\)
Bài 2:
a. Chứng minh rằng: \(1-\frac{1}{2^2}-\frac{1}{3^2}-\frac{1}{4^2}-...-\frac{1}{2011^2}>\frac{1}{2011}\)
b. Cho \(\left(5a_1+7b_1\right)^{2010}+\left(5a_2+7b_2\right)^{2012}+\left(5a_3+7b_3\right)^{2014}\le0\) và \(b_1,b_2,b_3\ne0,b_1+b_2+b_3\ne0\) . Chứng minh rằng: \(\frac{a_1+a_2+a_3}{b_1+b_2+b_3}=-1\frac{2}{5}\)
Bài 3:
a. Cho \(\frac{x}{y}=\frac{z}{t}\) . Chứng minh rằng \(\frac{x^2-y^2}{z^2-t^2}=\left(\frac{y-x}{t-z}\right)^2=\frac{xy}{zt}\)
b. Độ dài 3 đường cao của 1 tam giác tỉ lệ với 3; 5; 6. Tính độ dài 3 cạnh tương ứng của tam giác đó, biết rằng chu vi của tam giác là 42cm
c. Chứng minh rằng \(2^{x+4}-3^x-3^{x+2}-2^x\) chia hết cho 30 với x la số tựu nhiên lớn hơn hoặc bằng 1