L trên BC của tam giác ABC thỏa mãn AL có độ dài gấp đôi đường trung tuyến CM. Giả sử góc ALC= 45 độ. CMR Al vuông CM
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
14 tháng 2 2020
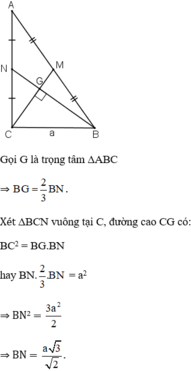
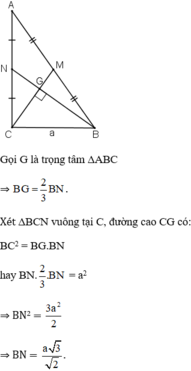
Gọi \(K\) là trung điểm của \(AL\Rightarrow MK\) là đường trung bình của \(\Delta ABL\)
\(\Rightarrow AK=KL=\frac{1}{2}AL\) và \(MK//BL\)
Theo định lí ta-lét ta có:
\(\frac{KO}{OL}=\frac{MO}{OC}\Rightarrow\frac{OK+OL}{OL}=\frac{MO+OC}{OC}\Rightarrow\frac{KL}{OL}=\frac{MC}{OC}\)
Lại có: \(KL=MC\Rightarrow OL=OC\)
\(\Rightarrow\Delta OCL\) cân tại \(O\)
Mà: \(\widehat{ALC}=45^0\)
\(\Rightarrow\Delta OCL\) vuông cân tại \(O\)
\(\Rightarrow AL\perp CM\left(đpcm\right)\)
22 tháng 12 2021
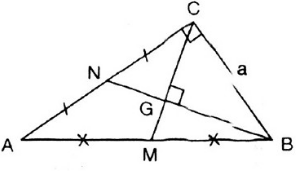
a) xét tg AMC và tg ABN có
MA=BA(gt)
CA=AN(gt)
ˆMAC=ˆBAN(doˆMAB+ˆBAC=ˆNAC+ˆBAC)MAC^=BAN^(doMAB^+BAC^=NAC^+BAC^)
=>(kết luận)...
b)gọi I là giao điểm của MC và BN
gọi giao điểm của BA và MI là F
vì ΔAMC=ΔABNΔAMC=ΔABNnên
ˆFMA=ˆFBIFMA^=FBI^
mà ˆFMA+ˆFMB=45OFMA^+FMB^=45O
=>ˆFBI+ˆIMB=45OFBI^+IMB^=45O
Xét ΔIMBΔIMBcó góc ˆIMB+ˆMBI+ˆBIMIMB^+MBI^+BIM^= 180O
Mà ˆIMB+ˆMBIIMB^+MBI^=900
=>...