Cho (O, R) có đường kính AB. Trên tia đối của tia AB lấy điểm E sao cho AE bằng một nửa bán kính. Từ E vẽ tiếp tuyến EM của (O) với M là tiếp điểm; tiếp tuyến tại A và B của (O) cắt đường thẳng EM tại C và D a, CMR: tam giác AMB vuông và AC+BD=CDb, OC cắt AM tại H và OD cắt MB tại K. C/m tứ giác mhok là hcnc, C/m: MA.OD=MB.OCd, Tính diện tích hình thang ABDC theo RChỉ cần làm câu...
Đọc tiếp
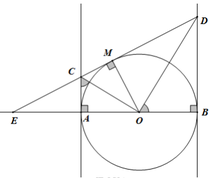
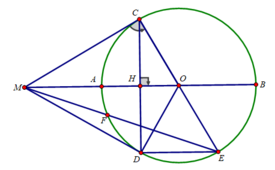
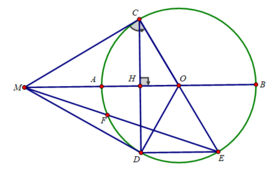
Cho (O, R) có đường kính AB. Trên tia đối của tia AB lấy điểm E sao cho AE bằng một nửa bán kính. Từ E vẽ tiếp tuyến EM của (O) với M là tiếp điểm; tiếp tuyến tại A và B của (O) cắt đường thẳng EM tại C và D
a, CMR: tam giác AMB vuông và AC+BD=CD
b, OC cắt AM tại H và OD cắt MB tại K. C/m tứ giác mhok là hcn
c, C/m: MA.OD=MB.OC
d, Tính diện tích hình thang ABDC theo R
Chỉ cần làm câu d
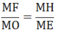
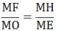
bạn có thể cho mình xem đáp án câu a b c đc k bạn
a, (O, R) có EM là tiếp tuyến ( M là tiếp điểm)
=> OM= R, EM\(\perp\)OM tại M
(O, R) có AB là đk
=> O là TĐ của AB
=> OA=OB=1/2AB=R
Tam giác AMB có MO là đường trung tuyến ứng với AB, MO=R=1/2AB
=> Tam giác AMB vuông tại M
C/ M các tiếp tuyến AC, CM cắt nhau => AC=CM
BD, MD cắt nhau => BD=MD
=> AC+BD=CM+MD=CD
b, Có OA=OM=R, AC=CM
=> OC là đường trung trực của AM
Mà OC cắt AM tại H
=> OC vuông với AM tại H, H là TĐ của AM.
C/M T.T: OD vuông với MB tại K, K là TĐ của MB.
T/g OKMH có 3 góc vuông AMB, OHM, OKM nên là hcn
c, DO là p/g góc MDB => MDO=ODB=1/2 MDB
OBD=90=> OBK+KBD=90
Tam giác DKB vuông tại K=> KBD+BDK=90
=> BDK=OBK
mà BDK=ODM=> OBK=ODM => ABM=ODC
C/m OC, OD lần lượt là p/g AOM, MOB . Từ đó c/m COD=90
C/m Tam giác ABM đồng dạng với tam giác CDO (gg)
=> AM/CO=BM/DO
=> AM.DO=MB.CO