Tìm m để hàm số y = - x2 + 2mx + 1 đồng biến trên khoảng \(\left(-\infty;3\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
K
2 tháng 8 2020
Ta có \(y'=\frac{x^2-2mx+m^2}{\left(x-2m\right)^2},x\ne2m\)
Để y có hai khoảng đồng biến trên toàn miền xác định thì
\(y'\ge0,\forall x\ne2m\)
\(\Leftrightarrow x^2-4mx+m^2\ge0,\forall x\ne2m\)
\(\Leftrightarrow\Delta'\le0\Leftrightarrow4m^2-m^2\le0\)
\(\Leftrightarrow3m^2\le0\Leftrightarrow m=0\)
Câu tiếp theo:
y đồng biến trên\(\left(1,\infty\right)\Leftrightarrow y'\ge0,\forall x\in\left(1,+\infty\right)\)
\(\Leftrightarrow\hept{\begin{cases}f\left(x\right)=x^2-4mx+m^2\ge0,\forall x>1\\2m\notin\left(1,\infty\right)\end{cases}}\)
Để cj suy nghĩ mai lm tiếp=.=
K
2 tháng 8 2020
rõ ràng m=0 thì đk trên thõa mãn.
Với \(m=0:\Delta'=3m^2>0\) nên ta có:
\(f\left(x\right)\ge0,\forall x>1\Leftrightarrow x_1< x_2\le1\)
\(\Leftrightarrow\hept{\begin{cases}\Delta'>0\\f\left(1\right)\ge\\\frac{S}{2}-1< 0\end{cases}0}\)
\(f\left(1\right)\ge0\Leftrightarrow m^2-4m+1\ge0\Leftrightarrow m\le2-\sqrt{3}\)hay\(m\ge2+\sqrt{3}\)
\(\frac{S}{2}-1< 0\Leftrightarrow2m-1< 0\Leftrightarrow m< \frac{1}{2}\)
\(2m\notin\left(1,\infty\right)\Leftrightarrow2m\le1\Leftrightarrow m\le\frac{1}{2}\)
Vậy \(m\le2-\sqrt{3}\)là giá trị m cần tìm
YN
10 tháng 1 2021
\(y=\left(m-1\right)x^2-2mx+m+2\)(1)
+) Nếu \(m-1=0\Leftrightarrow m=1\)thì :
(1) \(\Leftrightarrow y=-2x+3\)là hàm số bậc nhất có hệ số góc \(-2< 0\Rightarrow\)hàm số nghịch biến trên \(R\)
=> Hàm số nghịch biến trên \(\left(-\infty;2\right)\)
Vậy khi \(m=1\)hàm số nghịch biến trên \(\left(-\infty;2\right)\)(2)
+) Nếu \(m-1\ne0\Leftrightarrow m\ne1\)thì (1) là hàm số bậc hai
(1) nghịch biến trên \(\left(-\infty;2\right)\)thì đồ thị h/s có bề lõm hướng lên trên
\(\Rightarrow\hept{\begin{cases}a=m-1>0\\-\frac{b}{2a}\ge2\end{cases}}\Leftrightarrow\hept{\begin{cases}m>1\\\frac{2m}{2\left(m-1\right)}\ge2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}m>1\\m-2\left(m-1\right)\ge0\end{cases}}\Leftrightarrow\hept{\begin{cases}m>1\\m\le2\end{cases}}\)
\(\Rightarrow1< m\le2\)\(\Leftrightarrow\hept{\begin{cases}m>1\\m-2\left(m-1\right)\ge0\Leftrightarrow\hept{\begin{cases}m>1\\m\le2\end{cases}}\end{cases}}\)(3)
Từ (2) và (3) suy ra hàm số nghịch biến trên \(\left(-\infty;2\right)\)thì \(1\le m\le2\)
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 1 2021
- Với \(m=0\) thỏa mãn
- Với \(-2\left(4m-1\right)\ge0\Rightarrow m\le\dfrac{1}{4}\) hàm đồng biến trên \(\left(0;+\infty\right)\) thỏa mãn
- Xét với \(m>\dfrac{1}{4}\)
\(y'=4m^2x^3-4x\left(4m-1\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{\sqrt{4m-1}}{m}\\x=-\dfrac{\sqrt{4m-1}}{m}\end{matrix}\right.\)
Do \(a=m^2>0\) nên hàm đồng biến trên các khoảng \(\left(-\dfrac{\sqrt{4m-1}}{m};0\right)\) và \(\left(\dfrac{\sqrt{4m-1}}{m};+\infty\right)\)
\(\Rightarrow\) Hàm đồng biến trên khoảng đã cho khi và chỉ khi:
\(\dfrac{\sqrt{4m-1}}{m}\ge1\Rightarrow4m-1\ge m^2\)
\(\Leftrightarrow m^2-4m+1\le0\Rightarrow2-\sqrt{3}\le m\le2+\sqrt{3}\)
Vậy \(\left[{}\begin{matrix}m\le\dfrac{1}{4}\\2-\sqrt{3}\le m\le2+\sqrt{3}\end{matrix}\right.\)
CM
18 tháng 3 2018
TXĐ: D = R ∖ 2 m
y ' = - x 2 + 4 m x - m 2 x - 2 m 2 = f x x - 2 m 2
Đặt t = x - 1. Khi đó bất phương trình f x ≤ 0 trở thành g t = - t 2 - 2 1 + 2 m t - m 2 + 4 m - 1 ≤ 0
Hàm số nghịch biến trên 1 ; + ∞ khi và chỉ khi
y ' ≤ 0 , ∀ x ∈ 1 ; + ∞ ⇔ 2 m < 1 g t ≤ 0 , ∀ t > 0 * * ⇔ ∆ ' = 0 ∆ ' = 0 S < 0 P ≥ 0 ⇔ m = 0 m ≠ 0 4 m - 2 < 0 m 2 - 4 m + 1 ≥ 0 ⇔ m ≤ 2 - 3
Vậy m ≤ 2 - 3
Đáp án C
CM
10 tháng 3 2019
Đáp án B
Ta có y ' = 3 x 2 + 2 m x + 1 − 2 m
Hàm số đồng biến trên − 3 ; 0 ⇔ y ' ≥ 0 , ∀ x ∈ − 3 ; 0 ⇔ 3 x 2 + 2 m x + 1 − 2 m ≥ 0 , ∀ x ∈ − 3 ; 0
⇔ m 2 x − 2 ≥ − 3 x 2 − 1 ⇔ m ≤ − 3 x 2 + 1 2 x − 2 , x ∈ − 3 ; 0 1
Xét hàm số
f x = − 3 x 2 + 1 2 x − 2 , x ∈ − 3 ; 0 ⇒ f ' x = − 6 x 2 + 12 x + 2 2 x − 2 2 ⇒ f ' x = 0 ⇔ x = 3 ± 2 3 3
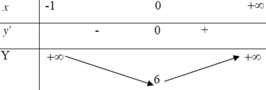
Ta có bảng biến thiên hàm số f x như sau:
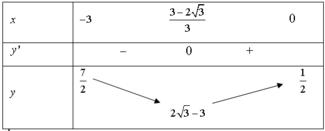
Suy ra f x − 3 ; 0 ≥ 2 3 − 3 ⇒ 1 ⇔ m ≤ 2 3 − 3
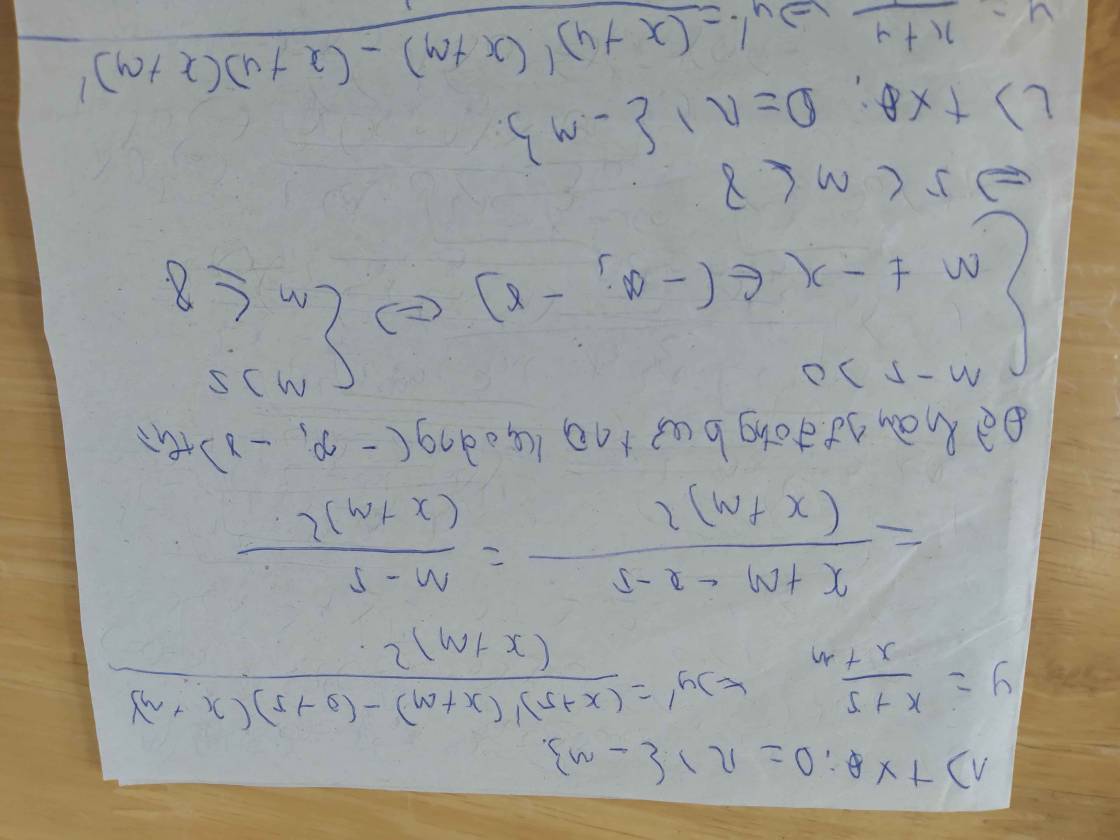
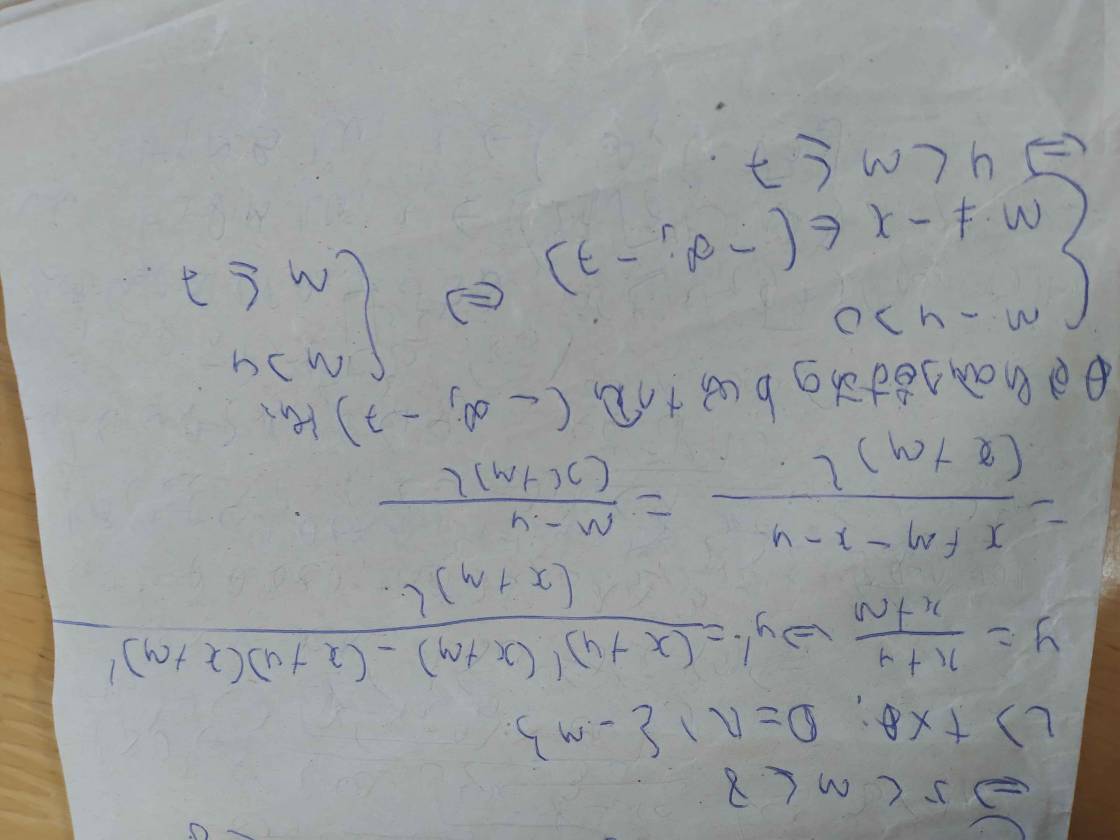
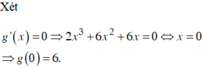
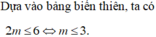
Hàm số \(y=-x^2+2mx+1\) có \(a=-1< 0;-\frac{b}{2a}=m\)nên đồng biến trên \(\left(-\infty;m\right)\)
Do đó để hàm số đồng biến trên khoảng \(\left(-\infty;3\right)\)thì ta phải có \(\left(-\infty;3\right)\subset\left(-\infty;m\right)\Leftrightarrow m\ge3.\)