Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Với y = ( m - 2 ) x 3 + ( m - 2 ) x 2 - x + 1 ta có y ' = 3 ( m - 2 ) x 2 + 2 ( m - 2 ) x - 1
Hàm số đã cho nghịch biến trên R
⇔ m - 2 < 0 ∆ ' ≤ 0 ⇔ m < 2 m 2 - m - 2 ≤ 0 ⇔ m < 2 - 1 ≤ m ≤ 2 ⇔ 1 ≤ m ≤ 2

Chọn B
Phương pháp: Sử dụng đạo hàm của hàm hợp để tính đạo hàm.


Đáp án là C
Tập xác định : D = R \{m}
Ta có : y ' = 1 − m x − m 2
Hàm số nghịch biến trên khoảng (−¥;2) khi và chỉ khi y' <0, "x < 2, tức là : 1 − m < 0 m ≥ 2 ⇔ m ≥ 2 . Vậy tập giá trị m cần tìm là [2; + ∞ )




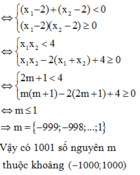

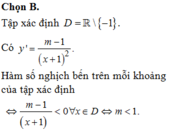
TXĐ: D = R ∖ 2 m
y ' = - x 2 + 4 m x - m 2 x - 2 m 2 = f x x - 2 m 2
Đặt t = x - 1. Khi đó bất phương trình f x ≤ 0 trở thành g t = - t 2 - 2 1 + 2 m t - m 2 + 4 m - 1 ≤ 0
Hàm số nghịch biến trên 1 ; + ∞ khi và chỉ khi
y ' ≤ 0 , ∀ x ∈ 1 ; + ∞ ⇔ 2 m < 1 g t ≤ 0 , ∀ t > 0 * * ⇔ ∆ ' = 0 ∆ ' = 0 S < 0 P ≥ 0 ⇔ m = 0 m ≠ 0 4 m - 2 < 0 m 2 - 4 m + 1 ≥ 0 ⇔ m ≤ 2 - 3
Vậy m ≤ 2 - 3
Đáp án C