cho hệ pt: \(x+my=2\)
\(mx-2y=1\)
tìm số nguyên m để hệ có nghiệm duy nhất (x;y) mà x,y là các số nguyên
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 3 2017
Chọn A
TH1. Nếu m+ 3< 0 hay m< - 3.Khi đó :
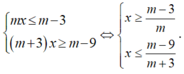
Hệ bất phương trình có nghiệm duy nhất
TH2. Nếu m+3= 0 hay m= -3
Khi đó :
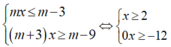
Hay x ≥ -2. Khi đó hệ bpt có vô số nghiệm (loại)
TH3. Nếu m+ 3> 0 hay m> - 3
+ Nếu -3< m< 0
Khi đó :
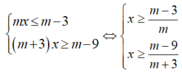
Hệ này có vô số nghiệm ( loại )
+ Nếu m= 0
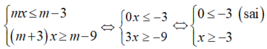
Hệ bất phương trình vô nghiệm( loại)
+ Nếu m> 0
Khi đó :
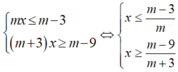
Hệ bất phương trình có nghiệm duy nhất
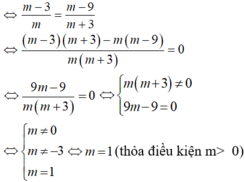
Vậy m= 1 thỏa yêu cầu bài toán.
15 tháng 6 2015
1, thay m=-2 vào giải chắc bạn làm đc nếu k liên hệ mình giải cho
b, giải sử pt có 2 nghiệm pb, áp dụng hệ thức vi ét ta có: \(x1+x2=2m+2\); \(x1.x2=m-2\Leftrightarrow2.x1.x2=2m-4\)
=> \(x1+x2-2.x1.x2=2m+2-2m+4=6\)=> hệ thức liên hệ k phụ thuộc vào m
2) \(\Delta=4\left(m-3\right)^2+4>0\) với mọi m=> pt luôn có 2 nghiệm pb
áp dụng hệ thức vi ét ta có: \(x1+x2=2m-6\); \(x1.x2=-1\)
câu này bạn xem có sai đề k. loại bài toán áp dụng hệ thức vi ét này k bao giờ có đề là x1-x2 đâu nha
sửa đề rồi liên hệ để mình làm tiếp nha
16 tháng 9 2016
\(\hept{\begin{cases}x-y=1\\3x+2y=m\end{cases}\Leftrightarrow}\hept{\begin{cases}2x-2y=2\\3x+2y=m\end{cases}}\) \(\Rightarrow5x=m+2\Rightarrow x=\frac{m+2}{5}\)
thay \(y=x-1=\frac{m+2}{5}-1=\frac{m-3}{5}\)
Vì \(\frac{x}{y}=\frac{3}{4}\Rightarrow x=\frac{3y}{4}\Rightarrow\frac{m+2}{5}=3\left(\frac{m-3}{20}\right)\Leftrightarrow m=-17\)
Vậy m = -17
x = 2 -my (1)
(2) => m( 2 - my) - 2y = 1
=> (m2+2) y = 2m -1 (*)=> pt luôn có nghiệm duy nhất => \(y=\frac{2m-1}{m^2+2}\in Z\)
(*) => y m2 -2m +2y -1 =0
+ y =0 => x =2 ; m =-1/2
+y \(\ne\)0 => \(\Delta\)' =1 - 2y2 +y >/ 0 => -1/2 </ y </ 1
=> y =o loại ; y =1
với y =1 => m= 1 => x =1 (tm)
Vậy m= -1/2 => (x;y) =(2;0)
m =1 => (x;y) =(1;1)