Dạng 1: Tính giá trị biểu thức [Rút gọn biểu thức rồi thay số (nếu đc)]
1) Tính giá trị biểu thức B = \(\sqrt{x-1+2\sqrt[3]{x\sqrt{x}+3x+3\sqrt{x}+1}}\), vs x = 5
2) Tính giá trị biểu thức C = \(\sqrt{2x-1+2\sqrt{x^2-x}+\sqrt{2x-1-2\sqrt{x^2-x}}}\), vs x = 4
3) Tính giá trị biểu thức D = \(\frac{\sqrt[3]{x\sqrt{x}\left(3x+1\right)+x^2\left(3+x\right)}}{\sqrt{x}+1}-\sqrt{x}\), vs x = 10
4) Tính giá trị biểu thức E = \(\sqrt{\sqrt[4]{x}+1-2\sqrt[8]{x}+1}\), vs x = 256
5) Cho x = \(\frac{\left(\sqrt{5}+2\right)\sqrt{3\sqrt{5}-6}}{\sqrt{4+\sqrt{9-4\sqrt{5}}}}\), tính giá trị biểu thức A = \(\left(x^4-5x^2+5\right)^{2014}\)

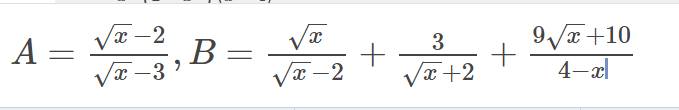
 và Q =
và Q =  (ĐKXĐ:
(ĐKXĐ: 
1) \(B=\sqrt{x-1+2\sqrt[3]{x\sqrt{x}+3x+3\sqrt{x}+1}}\)
\(B=\sqrt{x-1+2\sqrt[3]{\sqrt{x^3}+3x+3\sqrt{x}+1}}\)
\(B=\sqrt{x-1+2\sqrt[3]{\left(\sqrt{x}+1\right)^3}}\)
\(B=\sqrt{x-1+2\left(\sqrt{x}+1\right)}\)
\(B=\sqrt{x-1+2\sqrt{x}+2}\)
\(B=\sqrt{\left(\sqrt{x}+1\right)^2}\)
\(B=\sqrt{x}+1\)
\(B=\sqrt{5}+1\)
2) Sửa đề :
\(C=\sqrt{2x-1+2\sqrt{x^2-x}}+\sqrt{2x-1-2\sqrt{x^2-x}}\)
\(C=\sqrt{x+2\sqrt{x\left(x-1\right)}+x-1}+\sqrt{x-2\sqrt{x\left(x-1\right)}+x-1}\)
\(C=\sqrt{\left(\sqrt{x}+\sqrt{x-1}\right)^2}+\sqrt{\left(\sqrt{x}-\sqrt{x-1}\right)^2}\)
\(C=\sqrt{x}+\sqrt{x-1}+\sqrt{x}-\sqrt{x-1}\)
\(C=2\sqrt{x}\)
\(C=2\cdot\sqrt{4}=4\)
đợi tí lát solve full cho