Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Khi x=9 thì A=(9-2)/(3+2)=7/5
b: \(B=\dfrac{x-\sqrt{x}+2\sqrt{x}+2-4}{x-1}=\dfrac{x+\sqrt{x}-2}{x-1}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\)
c: P=A*B
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}+1}\cdot\dfrac{x-2}{\sqrt{x}+2}=\dfrac{x-2}{\sqrt{x}+1}\)
P=7/4
=>(x-2)/(căn x+1)=7/4
=>4x-8=7căn 7+7
=>4x-7căn x-15=0
=>căn x=3(nhận) hoặc căn x=-5/4(loại)
=>x=9

a) \(A=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}=1+\dfrac{4}{\sqrt{x}-2}\)
Để A nguyên thì 4 ⋮ √x - 2
\(\Rightarrow\sqrt{x}-2\inƯ\left(4\right)\)
\(\Rightarrow\sqrt{x}-2\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Rightarrow\sqrt{x}\in\left\{3;1;4;0;6;-2\right\}\)
Mà x \(\sqrt{x}\ge0\)
=> x thuộc {9; 1; 16; 0; 36}
b)

Lời giải:
a.
\(A=\frac{(x\sqrt{x}-4x)-(\sqrt{x}-4)}{2(\sqrt{x}-4)(\sqrt{x}-2)(\sqrt{x}-1)}\)
ĐKXĐ: \(\left\{\begin{matrix} x\geq 0\\ \sqrt{x}-4\neq 0\\ \sqrt{x}-2\neq 0\\ \sqrt{x}-1\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 0\\ x\neq 16\\ x\neq 4\\ x\neq 1\end{matrix}\right.\)
\(A=\frac{x(\sqrt{x}-4)-(\sqrt{x}-4)}{2(\sqrt{x}-4)(\sqrt{2}-2)(\sqrt{x}-1)}=\frac{(x-1)(\sqrt{x}-4)}{2(\sqrt{x}-4)(\sqrt{x}-2)(\sqrt{x}-1)}\)
\(=\frac{(\sqrt{x}-1)(\sqrt{x}+1)(\sqrt{x}-4)}{2(\sqrt{x}-4)(\sqrt{x}-2)(\sqrt{x}-1)}=\frac{\sqrt{x}+1}{2(\sqrt{x}-2)}\)
b.
Với $x$ nguyên, để $A\in\mathbb{Z}$ thì $\sqrt{x}+1\vdots 2(\sqrt{x}-2)}$
$\Rightarrow \sqrt{x}+1\vdots \sqrt{x}-2$
$\Leftrightarrow \sqrt{x}-2+3\vdots \sqrt{x}-2$
$\Leftrightarrow 3\vdots \sqrt{x}-2$
$\Rightarrow \sqrt{x}-2\in\left\{\pm 1;\pm 3\right\}$
$\Rightarrow x\in\left\{1;9;25\right\}$
Thử lại thấy đều thỏa mãn.

a) Ta có: \(P=\dfrac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\dfrac{2x+\sqrt{x}}{\sqrt{x}}+\dfrac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(=\sqrt{x}\left(\sqrt{x}-1\right)-2\sqrt{x}-1+2\left(\sqrt{x}+1\right)\)
\(=x-\sqrt{x}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(=x-\sqrt{x}+1\)

a: \(A=\dfrac{x\left(\sqrt{x}-4\right)-\left(\sqrt{x}-4\right)}{2x\sqrt{x}-8x-6x+24\sqrt{x}+4\sqrt{x}-16}\)
\(=\dfrac{\left(\sqrt{x}-4\right)\left(x-1\right)}{\left(\sqrt{x}-4\right)\left(2x-6\sqrt{x}+4\right)}=\dfrac{x-1}{2x-6\sqrt{x}+4}\)
\(=\dfrac{x-1}{2\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}+1}{2\sqrt{x}-4}\)
b: Để A nguyên thì \(2\sqrt{x}+2⋮2\sqrt{x}-4\)
\(\Leftrightarrow2\sqrt{x}-4\in\left\{2;-2;6\right\}\)
hay \(x\in\left\{9;1;25\right\}\)

a: Khi x=9 thì \(A=\dfrac{17}{3+2}=\dfrac{17}{5}\)
b: 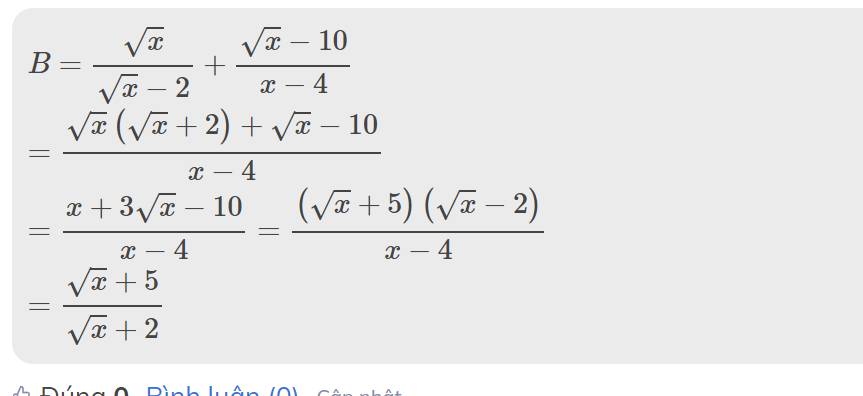
c: P=A:B
\(=\dfrac{17}{\sqrt{x}+2}:\dfrac{\sqrt{x}+5}{\sqrt{x}+2}=\dfrac{17}{\sqrt{x}+5}\)
Để P là số nguyên thì \(17⋮\sqrt{x}+5\)
mà \(\sqrt{x}+5>=5\) với mọi x thỏa mãn ĐKXĐ
nên \(\sqrt{x}+5=17\)
=>x=144
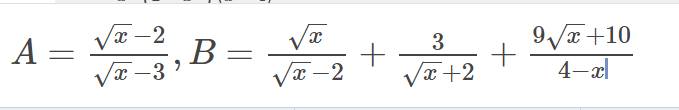
a: Khi x=16/9 thì \(A=\left(\dfrac{4}{3}-2\right):\left(\dfrac{4}{3}-3\right)=\dfrac{-2}{3}:\dfrac{-5}{3}=\dfrac{2}{5}\)
b: \(=\dfrac{x+2\sqrt{x}+3\sqrt{x}-6-9\sqrt{x}-10}{x-4}\)
\(=\dfrac{x-4\sqrt{x}-16}{x-4}\)