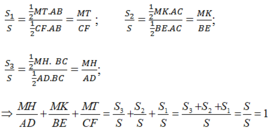Cho tam giác nhọn ABC , các đường cao AD , BE , CF cắt nhau tại H.Đường thẳng đi qua H song song BC cắt DE , DF tại I và K . Chứng minh tam giác IDK là tam giác cân
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TQ
13 tháng 6 2021
Xét tứ giác \(HECD\) có :
∠\(HEC=90^0\) ( Vì \(BE\)⊥\(AC\) )
∠\(HDC=90^0\) ( Vì \(AD\)⊥\(BC\) )
Mà 2 góc này đối nhau do đó :
Tứ giác \(HECD\) nội tiếp đường tròn => ∠\(HDE\)\(=\)∠\(HCE\) ( Cùng chắn cung \(HE\) )\(\left(1\right)\)
Tương tự :
Tứ giác \(HFBD\) cũng nội tiếp đường tròn ( Vì ∠\(HBF\)\(=90^0\) và ∠\(HDB=90^0\))
=> ∠\(HDF=\) ∠\(FBH\) ( Cùng chắn cung \(HF\) )\(\left(2\right)\)
Ta lại có :
∠\(CFB=\) ∠\(BEC\) \(=90^0\)
Mà 2 góc này cùng nhìn cạnh \(BC\) do đó :
Tứ giác \(EFBC\:\) nội tiếp đường tròn => ∠\(EBF\)\(=\) ∠\(ECF\) ( Cùng chắn cung \(EF\) )\(\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\) suy ra ∠\(IDH=\) ∠\(KDH\) hay \(DH\) là tia phân giác của △\(DIK\)\(\left(4\right)\)
Mặc khác : Đường thẳng qua \(H\)//BC => Đường thẳng đó ⊥ \(AD\) tại \(H\) hay \(DH\) là đường cao của △\(DIK\)\(\left(5\right)\)
Từ \(\left(4\right)\) và \(\left(5\right)\) suy ra △\(DIK\) cân =>\(đpcm\)
NN
27 tháng 4 2021
Ta có: AEH=90⁰.
=>HAE+AHE=90⁰.(1)
Ta có: ∆BHD vuông tại D.
=>DBH+BHD=90⁰.(2)
Từ (1) và (2) suy ra: HAE+AHE=DBH+BHD=90⁰.
Mà: AHE=DBH (2 góc đối đỉnh).
=> HAE=DBH.
=>HAE=DBE.
=>∆HEA~CBE(g.g).
=>AE/BE=HE/CE.
=>BE.HE=AE.CE.=>4BE.HE=4AE.CE.=>4BE.HE=AC².
=> (AE+CE)²=4AE.CE.
=>(AE-CE)²=0.
=>AE=CE
=> E là trung điểm của AC
=> BE là đường trung tuyến của ∆ABC
Mà: BE là đường cao của ∆ABC.
=> ∆ABC cân tại B.
DD
Đoàn Đức Hà
Giáo viên
13 tháng 7 2021
Xét tứ giác \(AIDK\):
\(AI//DK,AK//DI\)
Suy ra \(AIDK\)là hình bình hành.
mà \(AD\)là phân giác trong của góc \(\widehat{IAK}\)nên \(AIDK\)là hình thoi .
Suy ra \(DK=DI\)
do đó tam giác \(IDK\)là tam giác cân.
CM
5 tháng 11 2017
Gọi diện tích các hình tam giác ABC, MAB, MAC, MBC lần lượt là S, S 1 , S 2 , S 3 . Ta có:
S = S 1 + S 2 + S 3
Trong đó: S = 1/2 AD.BC = 1/2 BE. AC = 1/2 CF. AB
S 1 = 1/2 MT. AB
S 2 = 1/2 MK. AC
S 3 = 1/2 MH. BC
