giúp mình với ạ, bài 3 thôi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PM
1
21 tháng 8 2021
Bài 4:
ĐKXĐ: \(x\ge3\)
Ta có: \(\sqrt{x^2-9}-\sqrt{x-3}=0\)
\(\Leftrightarrow\sqrt{x-3}\left(\sqrt{x+3}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x+3=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\left(nhận\right)\\x=-2\left(loại\right)\end{matrix}\right.\)
7 tháng 10 2021
Bài 2:
Xét ΔABC vuông tại C có
\(CB=BA\cdot\sin60^0=12\cdot\dfrac{\sqrt{3}}{2}=6\sqrt{3}\left(cm\right)\)
18 tháng 10 2021
\(13,=\dfrac{\sqrt{3}\left(\sqrt{6}-2\right)}{\sqrt{6}-2}+\dfrac{4\left(\sqrt{3}-1\right)}{2}+12-3\sqrt{3}\\ =\sqrt{3}+2\sqrt{3}-2+12-3\sqrt{3}=10\\ 14,=\dfrac{12\left(4+\sqrt{10}\right)}{6}-3\sqrt{10}+\dfrac{\sqrt{10}\left(\sqrt{5}+1\right)}{\sqrt{5}+1}\\ =8+2\sqrt{10}-3\sqrt{10}+\sqrt{10}=8\\ 15,=\dfrac{2x-6\sqrt{x}+x+3\sqrt{x}-3x-9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\\ =\dfrac{-3\left(\sqrt{x}+3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{-3}{\sqrt{x}-3}\)
\(16,=\dfrac{x+2\sqrt{x}-3-x+3\sqrt{x}-4\sqrt{x}-6}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ =\dfrac{\sqrt{x}-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\\ 17,=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ =\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\)
25 tháng 8 2021
Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)
SV
Sinh Viên NEU
CTVVIP
26 tháng 11 2023
1 B
2 C
3 A
4 A
5 D
6 D
7 A
8 A
9 C
10 C
11 B
12 C
13 B
14 B
15 C
16 C
17 C
18 B
19 B
20 D
SV
Sinh Viên NEU
CTVVIP
26 tháng 11 2023
21 A
22 A
23 A
24 B
25 B
26 C
27 A
28 D
29 B
30 A
31 A
32 B
33 C
34 D
35 B
VN
11 tháng 1 2023
a)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x+y+z}{3+5+6}=\dfrac{98}{14}=7\)
\(+)\)\(\dfrac{x}{3}=7\Rightarrow x=7\times3=21\)
\(+)\)\(\dfrac{y}{5}=7\Rightarrow y=7\times5=35\)
\(+)\)\(\dfrac{z}{6}=7\Rightarrow z=7\times6=42\)
Vậy \(x=21;y=35;z=42\)
b)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{2}=\dfrac{x+y-z}{4+5-2}=\dfrac{21}{7}=3\)
\(+)\)\(\dfrac{x}{4}=3\Rightarrow x=3\times4=12\)
\(+)\)\(\dfrac{y}{5}=3\Rightarrow y=3\times5=15\)
\(+)\)\(\dfrac{z}{2}=3\Rightarrow z=3\times2=6\)
Vậy \(x=12;y=15;z=6\)
c)
Ta có :
\(x:y:z=5:\left(-6\right):7\) và \(x-y-z=16\)
\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{-6}=\dfrac{z}{7}\) và \(x-y-z=16\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{5}=\dfrac{y}{-6}=\dfrac{z}{7}=\dfrac{x-y-z}{5-\left(-6\right)-7}=\dfrac{16}{4}=4\)
\(+)\)\(\dfrac{x}{5}=4\Rightarrow x=4\times5=20\)
\(+)\)\(\dfrac{y}{-6}=4\Rightarrow y=4\times\left(-6\right)=-24\)
\(+)\)\(\dfrac{z}{7}=4\Rightarrow z=4\times7=28\)
Vậy \(x=20;y=-24;z=28\)
d)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{2}=\dfrac{y}{3}=\dfrac{z}{4}=\dfrac{x+z}{2+4}=\dfrac{18}{6}=3\)
\(+)\)\(\dfrac{x}{2}=3\Rightarrow x=3\times2=6\)
\(+)\)\(\dfrac{y}{3}=3\Rightarrow y=3\times3=9\)
\(+)\)\(\dfrac{z}{4}=3\Rightarrow z=3\times4=12\)
Vậy \(x=6;y=9;z=12\)
e)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\dfrac{x}{5}=\dfrac{y}{6}=\dfrac{z}{7}=\dfrac{x-y}{5-6}=\dfrac{36}{-1}=-36\)
\(+)\)\(\dfrac{x}{5}=-36\Rightarrow x=-36\times5=-180\)
\(+)\)\(\dfrac{y}{6}=-36\Rightarrow y=-36\times6=-216\)
\(+)\)\(\dfrac{z}{7}=-36\Rightarrow z=-36\times7=-252\)
Vậy \(x=-180;y=-216;z=-252\)
11 tháng 1 2023
a: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{3}=\dfrac{y}{5}=\dfrac{z}{6}=\dfrac{x+y+z}{3+5+6}=\dfrac{98}{14}=7\)
=>x=21; y=35; z=42
b: x/4=y/5=z/2 và x+y-z=21
Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{4}=\dfrac{y}{5}=\dfrac{z}{2}=\dfrac{x+y-z}{4+5-2}=\dfrac{21}{7}=3\)
=>x=12; y=15; z=6
c: Áp dụng tính chất của DTSBN, ta được:
\(\dfrac{x}{5}=\dfrac{y}{-6}=\dfrac{z}{7}=\dfrac{x-y-z}{5+6-7}=\dfrac{16}{4}=4\)
=>x=20; y=-24; z=28
d: Áp dụng tính chất của DTSBN, ta được:
x/2=y/3=z/4=(x+z)/(2+4)=18/6=3
=>x=6; y=9; z=12
PA
1
6 tháng 12 2021
Bài 8:
\(1,P=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-2-5\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3x-6\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\\ P=\dfrac{3\sqrt{x}\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\sqrt{x}}{\sqrt{x}+2}\\ 2,P=2\Leftrightarrow2\sqrt{x}+4=3\sqrt{x}\Leftrightarrow\sqrt{x}=4\\ \Leftrightarrow x=16\left(tm\right)\)
Bài 9:
\(a,M=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ M=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\left(\sqrt{x}-1\right)\\ M=\dfrac{x-1}{\sqrt{x}}\\ b,M>0\Leftrightarrow x-1>0\left(\sqrt{x}>0\right)\\ \Leftrightarrow x>1\)
Bài 10:
\(a,A=\dfrac{\sqrt{\left(x+3\right)^2}}{x+3}=\dfrac{\left|x+3\right|}{x+3}\)
Với \(x\ge-3\Leftrightarrow A=\dfrac{x+3}{x+3}=1\)
Với \(x< -3\Leftrightarrow A=\dfrac{-\left(x+3\right)}{x+3}=-1\)
\(b,B=\dfrac{2}{x-1}\cdot\dfrac{\left|x-1\right|}{2\left|x\right|}\)
Với \(0< x< 1\Leftrightarrow B=\dfrac{2}{x-1}\cdot\dfrac{-\left(x-1\right)}{2x}=-\dfrac{1}{x}\)
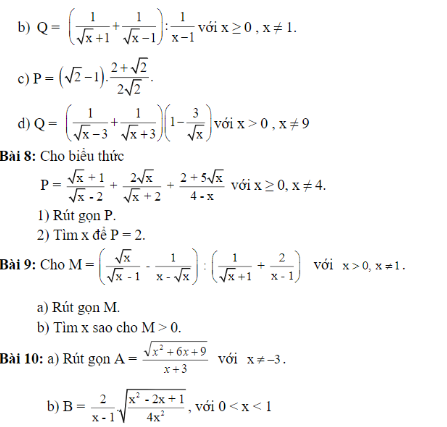
OK mình sẽ giúp
Ok mk ko biết làm
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////********************************************************************************************************************************************************************************************************************************************************************************************************************