Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Vì \(AH\), \(CK\) vuông góc với \(BD\) (gt)
Suy ra \(AH\) // \(CK\)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Xét \(\Delta ADH\) và \(\Delta CBK\) ta có:
\(\widehat {{\rm{AHD}}} = \widehat {{\rm{CKB}}} = 90^\circ \) (gt)
\(AD = BC\) (cmt)
\(\widehat {{\rm{ADH}}} = \widehat {{\rm{CBK}}}\) (do \(AD\) // \(BC\))
Suy ra \(\Delta ADH = \Delta CBK\) (ch-gn)
Suy ra \(AH = CK\) (hai cạnh tương ứng)
Mà \(AH\) // \(CK\) (cmt)
Suy ra \(AHCK\) là hình bình hành
b) Vì \(AHCK\) là hình bình hành nên hai đường chéo \(HK\) và \(AC\) cắt nhau tại trung điểm.
Mà \(I\) là trung điểm của \(HK\).
Suy ra \(I\) là trung điểm của \(AC\).
Ta lại có \(ABCD\) là hình bình hành nên hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm.
Suy ra \(I\) là trung điểm của \(BD\) hay \( IB = ID\)
a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
\(\widehat{ADH}=\widehat{CBK}\)
Do đó: ΔAHD=ΔCKB
Suy ra: AH=CK
Xét tứ giác AHCK có
AH//CK
AH=CK
Do đó: AHCK là hình bình hành
b: Ta có: AHCK là hình bình hành
nên Hai đường chéo AC và HK cắt nhau tại trung điểm của mỗi đường
mà O là trung điểm của HK
nên O là trung điểm của AC
hay A,O,C thẳng hàng
b) Xét hai tam giác vuông AHD và CKB có:
AD=BC
góc ADB=góc DBC (so le trong).
=> tam giác AHD=tam giác CKB (ch-gn)
=> BH=CK( hai cạnh tương ứng)
Lấy M trung điểm BD , nên MD=MB => MD-DH=MB-BK=> MH=MK, nên M Trung điểm HK
Vì ABCD là hình bình hành nên AC cắt BD tại trung điểm M.
Hay M là Trung điểm AC, mà M trung điểm HK.
Nên AKCH là hình bình hành.
a: Xét ΔAHD vuông tại H và ΔCKB vuông tại K có
AD=CB
góc ADH=góc CBK
=>ΔAHD=ΔCKB
=>AH=CK
mà AH//CK
nên AHCK là hình bình hành
b: AHCK là hbh
=>AC cắt HK tại trung điểm của mỗi đường
=>A,O,C thẳng hàng
\(a,\) Vì M là trung điểm AC và BD nên ABCD là hình bình hành
\(b,\) Vì ABCD là hình bình hành nên \(AD//BC;AD=BC\)
Do đó \(AK//CH;AK=CH(\dfrac{1}{2}AD=\dfrac{1}{2}BC)\)
Do đó AHCK là hình bình hành
Mà \(\Delta ABC\) cân tại A nên trung tuyến AH cũng là đường cao
Do đó \(AH\bot HC\)
Vậy AHCK là hình chữ nhật
\(c,\) Vì AHCK là hình chữ nhật nên trung điểm M của AC cũng là trung điểm của HK
Vậy H,M,K thẳng hàng
\(d,\) Để AHCK là hình vuông thì \(HK\bot AC\) tại M
Mà H,K là trung điểm BC,AC nên HK là đtb \(\Delta ABC\)
Do đó \(HK//AB\)
Mà \(HK\bot AC\) nên \(AC\bot AB\)
Vậy nếu tam giác ABC vuông cân tại A thì AHCK là hình vuông
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
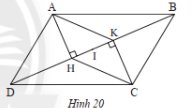
Câu 1:
a) Xét ΔAHD và ΔCKB có:
AD = BC (gt)
góc ADB = góc DBC ( SLT).
=> ΔAHD = ΔCKB (cạnh huyền- góc nhọn)
=> BH = CK( hai cạnh tương ứng)
Lấy M trung điểm BD
=> MD = MB
=> MD - DH = MB - BK
=> MH = MK (vì M Trung điểm HK)
Vì ABCD là hình bình hành nên AC cắt BD tại trung điểm M.
Hoặc M là Trung điểm AC và M trung điểm HK.
=> Tứ giác AKCH là hình bình hành (đpcm)
nguồn:Cho hình bình hành ABCD...