cứu e

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tóm tắt:
\(m_1=400g=0,4kg\)
\(t_1=100^oC\)
\(m_2=500g=0,5kg\)
\(t_2=13^oC\)
\(t=20^oC\)
\(c_2=4200J/kg.K\)
==========
\(c_1=?J/kg.K\)
Nhiệt lượng mà miếng kim loại tỏa ra:
\(Q_1=m_1.c_1.\Delta t_1=m_1.c_1.\left(t_1-t\right)=0,4.c_1.\left(100-20\right)\)
Nhiệt lượng mà nước nhận vào:
\(Q_2=m_2.c_2.\Delta t_2=m_2.c_2.\left(t-t_2\right)=0,5.4200.\left(20-13\right)=14700J\)
Vì nhiệt lượng miếng kim loại tỏa ra bằng nhiệt lượng nước thu vào:
\(Q_1=Q_2\)
\(\Leftrightarrow0,4.c_1.80=14700\)
\(\Leftrightarrow c_1=\dfrac{14700}{0,4.80}\)
\(\Leftrightarrow c_1=460J/kg.K\)

Bài 1
a) \(2^{11}.64=2^{11}.2^6=2^{17}\)
Do \(16< 17\Rightarrow2^{16}< 2^{17}\)
Vậy \(2^{16}< 2^{11}.64\)
b) Do \(18>17\Rightarrow9^{18}>9^{17}\) (1)
\(9^{18}=\left(3^2\right)^{18}=3^{36}\)
Do \(36< 37\Rightarrow3^{36}< 3^{37}\)
\(\Rightarrow9^{18}< 3^{37}\) (2)
Từ (1) và (2) \(\Rightarrow9^{17}< 3^{37}\)
c) \(2^{333}=\left(2^3\right)^{111}=8^{111}\)
\(3^{222}=\left(3^2\right)^{111}=9^{111}\)
Do \(8< 9\Rightarrow8^{111}< 9^{111}\)
Vậy \(2^{333}< 3^{222}\)
d) \(3^{50}=\left(3^2\right)^{25}=9^{25}\)
Do \(9< 11\Rightarrow9^{25}< 11^{25}\)
Vậy \(3^{50}< 11^{25}\)
e) \(37< 38\Rightarrow3^{37}< 3^{38}\) (1)
Lại có: \(3^{38}=3^{2.19}=\left(3^2\right)^{19}=9^{19}\)
Do \(9< 10\Rightarrow9^{19}< 10^{19}\)
\(\Rightarrow3^{38}< 10^{19}\) (2)
Từ (1) và (2) \(\Rightarrow3^{37}< 10^{19}\)
f) Do \(17>16\Rightarrow17^{14}>16^{14}\) (1)
Do \(32>31\Rightarrow32^{11}>31^{11}\) (2)
Lại có:
\(16^{14}=\left(2^4\right)^{14}=2^{56}\)
\(32^{11}=\left(2^5\right)^{11}=2^{55}\)
Do \(56>55\Rightarrow2^{56}>2^{55}\)
\(\Rightarrow16^{14}>32^{11}\) (3)
Từ (1), (2) và (3) \(\Rightarrow17^{14}>31^{11}\)
Bài 2:
a) \(2^n-64=0\)
\(2^n=64\)
\(2^n=2^6\)
\(n=6\)
b) \(5.3^{n-3}-405=0\)
\(5.3^{n-3}=405\)
\(3^{n-3}=405:5\)
\(3^{n-3}=81\)
\(n-3=4\)
\(n=4+3\)
\(n=7\)
c) \(4^n.8=2^{15}\)
\(\left(2^2\right)^n.2^3=2^{15}\)
\(2^{2n}.2^3=2^{15}\)
\(2^{2n+3}=2^{15}\)
\(2n+3=15\)
\(2n=15-3\)
\(2n=12\)
\(n=12:2\)
\(n=6\)
d) \(3.2^{n+1}+2^{n+2}=160\)
\(2^{n+1}.\left(3+2\right)=160\)
\(2^{n+1}.5=160\)
\(2^{n+1}=160:5\)
\(2^{n+1}=32\)
\(2^{n+1}=2^5\)
\(n+1=5\)
\(n=5-1\)
\(n=4\)

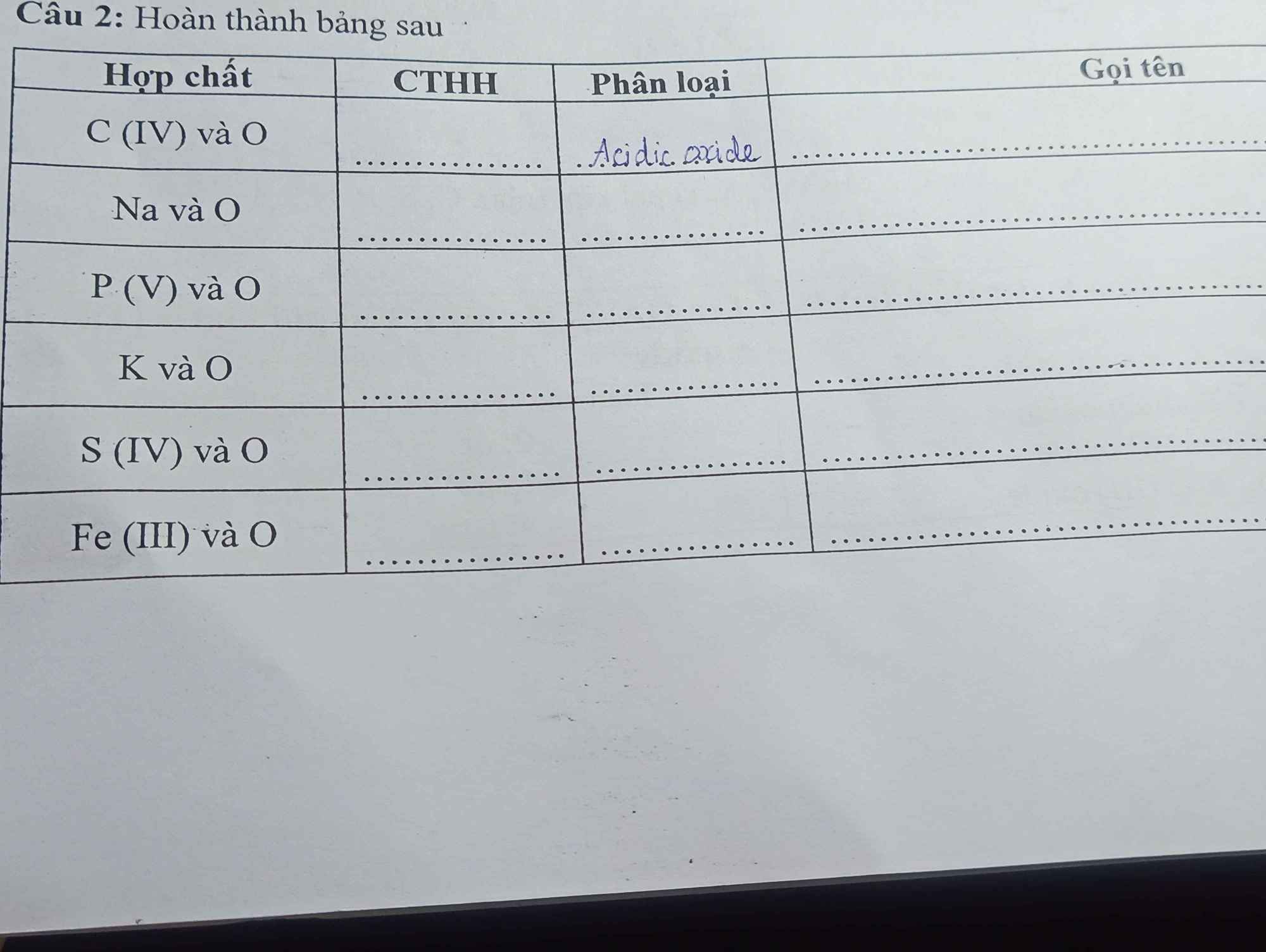
| Hợp chất | CTHH | Phân loại | Gọi tên |
| C(IV) và O | CO2 | oxit axit | Cacbon đioxit |
| Na và O | Na2O | oxit bazo | Natri oxit |
| P(V) và O | P2O5 | oxit axit | Điphotpho pentaoxit |
| K và O | K2O | oxit bazo | Kali oxit |
| S(IV) và O | SO2 | oxit axit | Lưu huỳnh đioxit |
| Fe(III) và O | Fe2O3 | oxit bazo | Sắt (III) oxit |

1:
a: Tiền vốn là:
1440000*5/6=1200000(đồng)
b: Số tiền lãi là:
1440000*20%=288000(đồng)
=>Số tiền vốn là:
1440000-288000=1152000(đồng)

12.
a. Do đường thẳng đi qua điểm A(-5;3) nên ta có:
\(-5a+b=3\) (1)
Do đường thẳng đi qua \(B\left(\dfrac{3}{2};-1\right)\) nên:
\(\dfrac{3}{2}a+b=-1\) (2)
Từ (1) và (2) ta có hệ: \(\left\{{}\begin{matrix}-5a+b=3\\\dfrac{3}{2}a+b=-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{8}{13}\\b=-\dfrac{1}{13}\end{matrix}\right.\)
b.
Gọi N là giao điểm (d1) và (d2), tọa độ N là nghiệm:
\(\left\{{}\begin{matrix}2x+5y=17\\4x-10y=14\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=6\\y=1\end{matrix}\right.\) \(\Rightarrow N\left(6;1\right)\)
Do đường thẳng đi qua M(9;-6) nên:
\(9a+b=-6\)
Do đường thẳng đi qua N(6;1) nên:
\(6a+b=1\)
Ta được hệ: \(\left\{{}\begin{matrix}9a+b=-6\\6a+b=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=-\dfrac{7}{3}\\b=15\end{matrix}\right.\)
13.
a.
Hai đường thẳng cắt nhau tại 1 điểm trên trục tung khi hoành độ giao điểm bằng 0
Tọa độ giao điểm 2 đường thẳng là nghiệm của hệ:
\(\left\{{}\begin{matrix}5x-2y=3\\x+y=m\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}5x-2y=3\\2x+2y=2m\end{matrix}\right.\)
\(\Rightarrow7x=2m+3\)
\(\Rightarrow x=\dfrac{2m+3}{7}\)
Hai đường thẳng cắt nhau trên trục tung nên:
\(\dfrac{2m+3}{7}=0\Rightarrow m=-\dfrac{3}{2}\)
Em tự vẽ hình
b.
Hai đường thẳng cắt nhau tại 1 điểm trên trục hoành khi tung độ giao điểm bằng 0.
Tọa độ giao điểm 2 đường thẳng là nghiệm:
\(\left\{{}\begin{matrix}mx+3y=10\\x-2y=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}mx+3y=10\\mx-2my=4m\end{matrix}\right.\)
Trừ vế cho vế \(\Rightarrow\left(2m+3\right)y=10-4m\)
2 đường thẳng cắt nhau khi \(2m+3\ne0\Rightarrow m\ne-\dfrac{3}{2}\)
Khi đó tung độ giao điểm là: \(y=\dfrac{10-4m}{2m+3}\)
2 đường cắt nhau trên trục hoành khi:
\(\dfrac{10-4m}{2m+3}=0\Rightarrow10-4m=0\)
\(\Rightarrow m=\dfrac{5}{2}\)




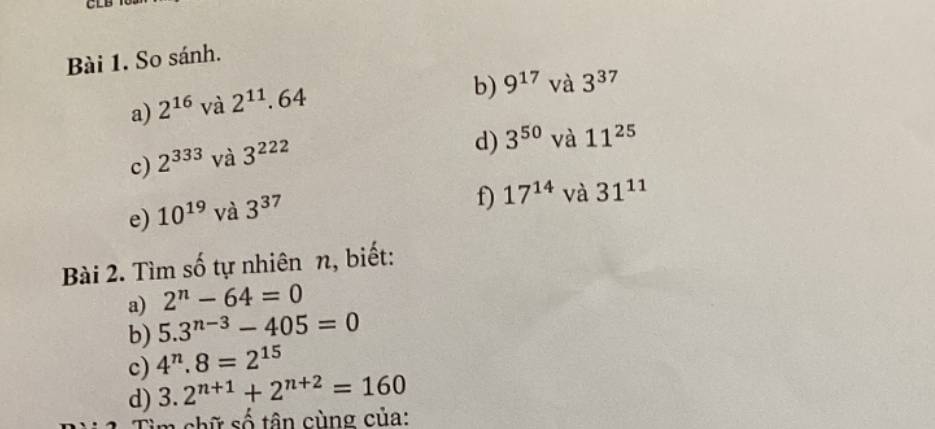


 sos cứu e
sos cứu e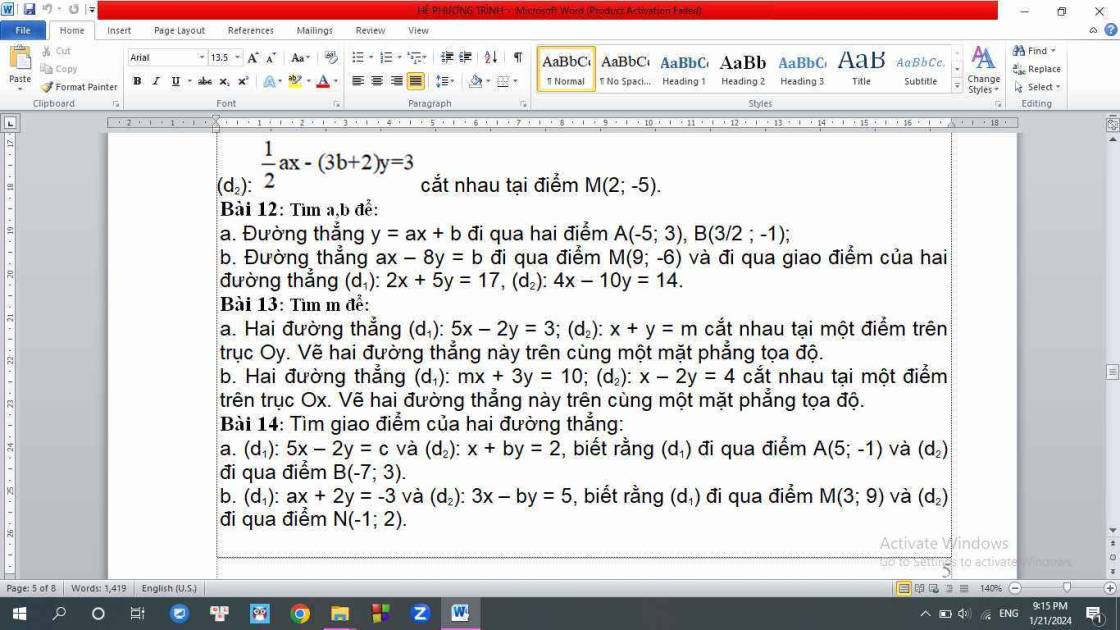 cứu e vssss
cứu e vssss
1 D
2 C
3 A
4 C
5 A
II
1 C
2 C
3 A
4 D
5 C
III
1 A
2 A
3 A
4 B
5 B
6 A
7 B
8 A
9 B
10 B
1 strong enough to lift that heavy luggage
2 intelligent enough to speak 4 languages
3 long black curly hair
4 2 hours watchingTV everyday
5 Bell invented the telephone