Cho khai triển (1+x+x2)20=a0+a1x+a2x2+...+a40x40 tính tổng T=a1+2a2+3a3+...+40a40
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
Ta có: 1 + x + x 2 − x 3 10 ' = a 0 + a 1 x + ... + a 30 x 30
' ⇔ 10 1 + x + x 2 − x 3 9 1 + x + x 2 − x 3
a 1 + 2 a 2 x + ... + 30 a 30 x 29 ⇔ 10 1 + x + x 2 − x 3 9 a 1 + 2 a 2 x + ... + 30 a 30 x 29
Chọn: x = 1 ⇒ 10 1 + 1 + 1 − 1 9 .0 = a 1 + 2 a 2 x + ... + 30 a 30
⇔ S = 0

Đáp án B
Đạo hàm ta hai vế ta được
10 1 + x + x 2 − x 3 9 . 1 + 2 x − 3 x 2 = a 1 + 2 a 2 x + ... + 30 a 30 x 29 Cho x = 1 ⇒ S = 0.

Chọn đáp án D
Ta có
![]()
nên a k = C n k ( - 2 ) k
⇒ a k = 2 k . C n k với 0 ≤ k ≤ n , k ∈ ℕ Suy ra
Xét khai triển
![]()
Đạo hàm hai vế của (*):

Nhân cả hai vế của (**) với x:
![]()
Thay x=2 vào (1) ta được
![]()
⇔ n . 3 n = 52488 = 8 . 3 8 . Suy ra n = 8
Vậy với n = 8 thì P = 390625


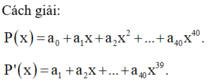
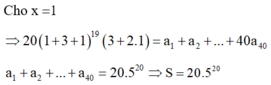
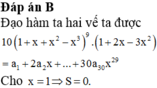



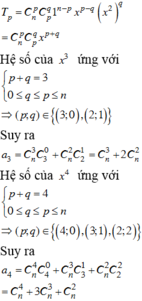
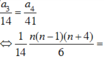
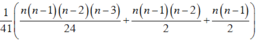
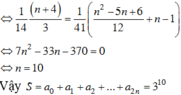
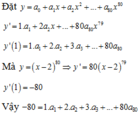
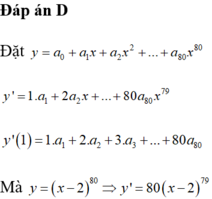
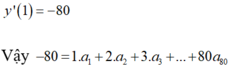
Gặp dạng hệ số đằng trước giống chỉ số của số hạng thế này thì cứ đạo hàm
\(\left(1+x+x^2\right)^{20}=a_0+a_1x+a_2x^2+...+a_{40}x^{40}\)
Đạo hàm 2 vế:
\(\Rightarrow20\left(1+x+x^2\right)^{19}\left(1+2x\right)=a_1+2a_2x+3a_3x^2+...+40a_{40}x^{39}\)
Cho \(x=1\) ta được:
\(20.3^{19}.3=a_1+2a_2+3a_3+...+40a_{40}\)
\(\Rightarrow T=20.3^{20}\)