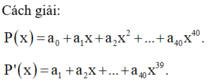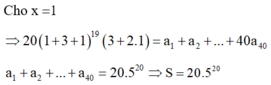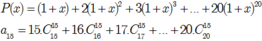Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gặp dạng hệ số đằng trước giống chỉ số của số hạng thế này thì cứ đạo hàm
\(\left(1+x+x^2\right)^{20}=a_0+a_1x+a_2x^2+...+a_{40}x^{40}\)
Đạo hàm 2 vế:
\(\Rightarrow20\left(1+x+x^2\right)^{19}\left(1+2x\right)=a_1+2a_2x+3a_3x^2+...+40a_{40}x^{39}\)
Cho \(x=1\) ta được:
\(20.3^{19}.3=a_1+2a_2+3a_3+...+40a_{40}\)
\(\Rightarrow T=20.3^{20}\)

\(A=x^2-x+1=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
\(\Rightarrow A_{min}=\frac{3}{4}\) khi \(x=\frac{1}{2}\), \(A_{max}\) ko tồn tại
\(B=x^2+2x+5=\left(x+1\right)^2+4\ge4\)
\(\Rightarrow B_{min}=4\) khi \(x=-1\) , \(B_{max}\) ko tồn tại
\(C=\left(5-x\right)^2+2017\ge2017\)
\(\Rightarrow C_{min}=2017\) khi \(x=5\) , \(C_{max}\) ko tồn tại
\(D=20-\left(2x+1\right)^2\le20\)
\(\Rightarrow D_{max}=20\) khi \(x=-\frac{1}{2}\), \(D_{min}\) ko tồn tại
\(E=x^2+2\left|y+1\right|+7\ge7\)
\(\Rightarrow E_{min}=7\) khi \(\left\{{}\begin{matrix}x=0\\y=-1\end{matrix}\right.\) , \(E_{max}\) ko tồn tại

\(\left(x^3+x^{-3}\right)^{18}=\sum\limits^{18}_{k=0}C^k_{18}.x^{3\left(18-k\right)}.x^{-3k}=\sum\limits^{18}_{k=0}C^k_{18}x^{54-6k}\)
Số hạng không chứa \(x\Rightarrow54-6k=0\Rightarrow k=9\)
Hệ số: \(C^9_{18}=48620\)
2/ Chọn ngẫu nhiên 7 quyển có \(C^7_{21}=116280\) cách
Các trường hợp có ít nhất 2 toán 2 lý 2 hóa: {3 toán 2 lý 2 hóa}; {2 toán 3 lý 2 hóa}; {2 toán 2 lý 3 hóa}
\(\Rightarrow\) có \(C^3_{10}.C^2_6.C^2_5+C^2_{10}.C^3_6.C^2_5+C^2_{10}.C^2_6.C^3_5=33750\) cách
Xác suất \(P=\dfrac{33750}{116280}=\dfrac{375}{1292}\)
Cách tính đúng rồi đấy, nhưng quá trình bấm máy thì bạn phải tự bấm lại cho chắc ăn

\(\left(1+x\right)\left(1+2x\right)...\left(1+nx\right)-1\)
\(=x+\sum\limits^n_{k=2}kx\left(1+x\right)...\left(1+\left(k-1\right)x\right)\)
\(=x+\sum\limits^n_{k=2}kx\left[\left(1+x\right)...\left(1+\left(k-1\right)x\right)-1+1\right]\)
\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left[\left(1+x\right)\left(1+2x\right)...\left(1+\left(k-1\right)x\right)-1\right]\)
\(=\sum\limits^n_{k=1}kx+\sum\limits^n_{k=2}kx\left(\sum\limits^{k-1}_{i=1}ix\left(1+x\right)\left(1+2x\right)...\left(1-\left(i-1\right)x\right)\right)\)
Do đó tổng của các hệ số chứa \(x^2\) là: \(\sum\limits^n_{k=2}k\left(\sum\limits^{k-1}_{i=1}i\right)\)
Hay \(a_2=\sum\limits^n_{k=2}k\left(\frac{k\left(k-1\right)}{2}\right)=\sum\limits^n_{k=2}\frac{k^2\left(k-1\right)}{2}\)
Do đó:
\(S=1+\sum\limits^{2019}_{k=2}\frac{k^2\left(k-1\right)}{2}+\sum\limits^{2019}_{k=2}k^2=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k-1\right)}{2}+k^2\right)\)
\(=1+\sum\limits^{2019}_{k=2}\left(\frac{k^2\left(k+1\right)}{2}\right)\)

ta có : \(P\left(x\right)=\sum\limits^{20}_{k=1}\left(2x+1\right)^k=\sum\limits^{20}_{k=1}C_k^p\left(2x\right)^{k-p}\left(1\right)^k\)
để có : \(x^5\Rightarrow k-p=5\)
\(\Rightarrow\) hệ số của \(P\left(x\right)\) trong khai triển là : \(\sum\limits^{20}_{k=1}C^p_k\left(2\right)^{k-p}=C^0_52^5+C^1_62^5+C^2_72^5+...+C^{15}_{20}2^5\)
\(=32\left(C^0_5+C^1_6+C^2_7+...+C^{15}_{20}\right)=32.54264=1736448\)
vậy hệ số của \(x^5\) trong khai triển đa thức \(P\left(x\right)\) là \(1736448\)

Đáp án đúng là: A
Dãy số 21; – 3; – 27; – 51; – 75 lập thành một cấp số cộng có số hạng đầu là u1 = 21 và công sai d = – 24.

a) gt \(\Leftrightarrow\) s-\(10\times\left(\frac{2}{11\times13}+\frac{2}{13\times15}+...+\frac{2}{53\times55}\right)=\frac{3}{11}\)
\(\Leftrightarrow s-10\times\left(\frac{1}{11}-\frac{1}{13}+\frac{1}{13}-\frac{1}{15}+...+\frac{1}{53}-\frac{1}{55}\right)=\frac{3}{11}\)
\(\Leftrightarrow S-10\times\left(\frac{1}{11}-\frac{1}{55}\right)=\frac{3}{11}\)
\(\Leftrightarrow S=1\)
câu b hình như sai đề
Phải là \(\frac{1}{36}\) chứ ko phải \(\frac{1}{39}\)