
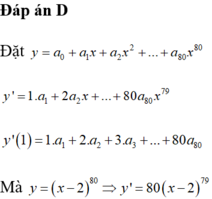
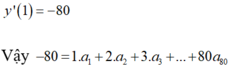
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

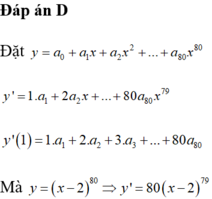
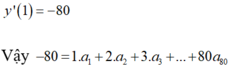

Xét khai triển:
\(\left(x+1\right)^n=C_n^0+C_n^1x+C_n^2x^n+C_n^3x^3+...+C_n^nx^n\)
Đạo hàm 2 vế:
\(n\left(x+1\right)^{n-1}=C_n^1+2C_n^2x+3C_n^3x^2+...+nC_n^nx^{n-1}\)
Thay \(x=1\) vào ta được:
\(n.2^{n-1}=C_n^1+2C_n^2+3C_n^3+...+nC_n^2=256n\)
\(\Rightarrow2^{n-1}=256=2^8\Rightarrow n=9\)
Câu 2:
\(\left(x-2\right)^{80}=a_0+a_1x+a_2x^2+a_3x^3+...+a_{80}x^{80}\)
Đạo hàm 2 vế:
\(80\left(x-2\right)^{79}=a_1+2a_2x+3a_3x^2+...+80a_{80}x^{79}\)
Thay \(x=1\) ta được:
\(80\left(1-2\right)^{79}=a_1+2a_2+3a_3+...+80a_{80}\)
\(\Rightarrow S=80.\left(-1\right)^{79}=-80\)

a/ Thiếu đề, sau dấu "-" hình như còn gì đó
b/ \(\Leftrightarrow\sqrt{2}sin\left(x+\frac{\pi}{4}\right)=1\Leftrightarrow sin\left(x+\frac{\pi}{4}\right)=\frac{1}{\sqrt{2}}=sin\left(\frac{\pi}{4}\right)\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\x+\frac{\pi}{4}=\frac{5\pi}{4}+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)
c/ \(\Rightarrow sin2x=-sinx\Leftrightarrow sin2x=sin\left(-x\right)\)
\(\Rightarrow\left[{}\begin{matrix}2x=-x+k2\pi\\2x=\pi+x+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\frac{k2\pi}{3}\\x=\pi+k2\pi\end{matrix}\right.\)
d/ \(\Leftrightarrow\left(sin^2x+cos^2x\right)^2-2\left(sinx.cosx\right)^2=1\)
\(\Leftrightarrow sinx.cosx=0\Leftrightarrow sin2x=0\)
\(\Rightarrow2x=k\pi\Rightarrow x=\frac{k\pi}{2}\)
e/ f/ Thiếu đề
g/ \(\Leftrightarrow\left[{}\begin{matrix}cos3x=cos2x\\cos3x=-cos2x\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}cos3x=cos2x\\cos3x=cos\left(\pi-2x\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}3x=2x+k2\pi\\3x=-2x+k2\pi\\3x=\pi-2x+k2\pi\\3x=2x-\pi+k2\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=k2\pi\\x=\frac{k2\pi}{5}\\x=\frac{\pi}{5}+\frac{k2\pi}{5}\\x=-\pi+k2\pi\end{matrix}\right.\)

Mình nhầm \(C^1_{2016}a_{2015}\)thành \(C^1_{2016}a^{2015}\)

\(cos2x=cos40\)
\(\Rightarrow\left[{}\begin{matrix}2x=40^0+k360^0\\2x=-40^0+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=20^0+k180^0\\x=-20^0+k180^0\end{matrix}\right.\)
\(cos3x=cos\left(x-80^0\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=x-80^0+k360^0\\3x=80^0-x+k360^0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-40^0+k180^0\\x=20^0+k90^0\end{matrix}\right.\)

\(\lim\limits_{x\rightarrow1}\frac{x^2+ax+b}{\left(x-1\right)\left(x+1\right)}=-\frac{1}{2}\) hữu hạn
\(\Rightarrow\) phương trình \(x^2+ax+b=0\) có 1 nghiệm bằng 1
\(\Leftrightarrow1+a+b=0\Rightarrow b=-a-1\)
\(\lim\limits_{x\rightarrow1}\frac{x^2+ax-a-1}{\left(x+1\right)\left(x-1\right)}=\lim\limits_{x\rightarrow1}\frac{\left(x+a+1\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\lim\limits_{x\rightarrow1}\frac{x+a+1}{x+1}=\frac{a+2}{2}\)
\(\Rightarrow\frac{a+2}{2}=-\frac{1}{2}\Rightarrow a=-3\Rightarrow b=2\)
\(\Rightarrow a^2+b^2=\left(-3\right)^2+2^2=13\)