tim x,y biet
1/5x-y=13
2/23x+53y=109
3/12x-5y=21
4/12x+17y=41
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
0
PT
0
OK
1
CM
1 tháng 1 2018
Cách 1
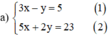
Từ (1) ta rút ra được y = 3x – 5 (*)
Thế (*) vào phương trình (2) ta được :
5x + 2(3x – 5) = 23 ⇔ 5x + 6x – 10 = 23 ⇔ 11x = 33 ⇔ x = 3.
Thay x = 3 vào (*) ta được y = 3.3 – 5 = 4.
Vậy hệ phương trình có nghiệm duy nhất (3 ; 4).
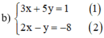
Từ (2) ta rút ra được y = 2x + 8 (*)
Thế (*) vào phương trình (1) ta được :
3x + 5(2x + 8) = 1 ⇔ 3x + 10x + 40 = 1 ⇔ 13x = -39 ⇔ x = -3.
Thay x = - 3 vào (*) ta được y = 2.(-3) + 8 = 2.
Vậy hệ phương trình có nghiệm duy nhất (-3 ; 2).
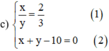
Từ (1) ta rút ra được x = 2 3 y (*)
Thế (*) vào phương trình (2) ta được :
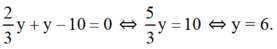
Thay y = 6 vào (*) ta được x = 4.
Vậy hệ phương trình có nghiệm duy nhất (x ; y) = (4 ; 6).
Cách 2
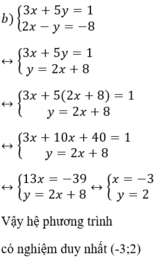
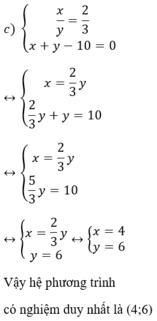
Kiến thức áp dụng
+ Giải hệ phương trình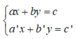 
ta làm như sau:
Bước 1: Từ một phương trình (coi là phương trình thứ nhất), ta biểu diễn x theo y (hoặc y theo x) ta được phương trình (*). Sau đó, ta thế (*) vào phương trình thứ hai để được một phương trình mới ( chỉ còn một ẩn).
Bước 2: Dùng phương trình mới ấy thay thế cho phương trình thứ hai, phương trình (*) thay thế cho phương trình thứ nhất của hệ ta được hệ phương trình mới tương đương .
Bước 3: Giải hệ phương trình mới ta tìm được nghiệm của hệ phương trình.
+ Nếu xuất hiện phương trình dạng 0x = a (hoặc 0y = a) thì ta kết luận hệ phương trình vô nghiệm nếu a ≠ 0 hoặc hệ có vô số nghiệm nếu a = 0.
BH
1
DD
Đoàn Đức Hà
Giáo viên
15 tháng 1 2023
a) \(\left(5,11\right)=1\) nên phương trình có vô số nghiệm.
Phương trình có một nghiệm là \(\left(3;1\right)\) nên nghiệm tổng quát của phương trình trên là
\(\left\{{}\begin{matrix}x=3+11t\\y=1+5t\end{matrix}\right.\), \(t \in \mathbb{Z}\).
b) \(\left(7,5\right)=1\) nên phương trình có vô số nghiệm.
Phương trình có một nghiệm là \(\left(4;23\right)\) nên nghiệm tổng quát của phương trình trên là
\(\left\{{}\begin{matrix}x=4+5t\\y=23-7t\end{matrix}\right.\), \(t \in \mathbb{Z}\).
c) Bạn đọc tự giải.
NT
0
1. Đơn giản hóa
5x + -1y = 13
Giải quyết
5x + -1y = 13
Giải cho biến 'x'.
Di chuyển tất cả các điều khoản có chứa x sang trái, tất cả các điều khoản khác sang phải.
Thêm 'y' vào mỗi bên của phương trình.
5x + -1y + y = 13 + y
Kết hợp như các điều khoản: -1y + y = 0
5x + 0 = 13 + y
5x = 13 + y
Chia mỗi bên cho '5'.
x = 2,6 + 0,2y
Đơn giản hóa x = 2,6 + 0,2y
P/s: Nguồn mạng Oppa :>>
Câu 3 tương tự ((:
C2:
Câu hỏi của Nguyễn Quế Dân - Toán lớp 6 - Học toán với OnlineMath
https://olm.vn/hoi-dap/detail/35109045377.html