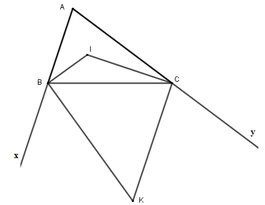
Cho tam giác ABC có góc A bằng 60 độ. Các phân giác ngoài của góc B và góc C cắt nhau tại K. Tính góc BKC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
30 tháng 7 2015
Trong tam giác ABC có góc BAC + ABC + ACB = 180 độ
\(\Rightarrow\) góc ABC + góc ACB = 180 độ - góc BAC = 180 độ - 60 độ = 120 (độ)
Ta có góc IBC + góc ICB = góc ABC/2 + góc ACB/2 = (góc ABC + góc ACB)/2 = 120 độ/2 = 60 (độ)
Trong tam giác IBC có góc BIC + góc IBC + góc ICB = 180 độ
\(\Rightarrow\) góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ
SU
31 tháng 7 2015
ai bit thi tra loi giup mik di mot chut nua la mik phai nop bai r
29 tháng 7 2019
http://pitago.vn/question/cho-tam-giac-abc-tia-phan-giac-cua-goc-b-cat-tia-phan-giac-49658.html
29 tháng 7 2019
a) Xét ∆ABC ta có :
ABC + ACB + BAC = 180°
=> ABC + ACB = \(180°\:-\:a\)
=> ABC + ACB = 110°
Vì BI là phân giác ABC
=> ABI = CBI
Vì CI là phân giác ACB
=> ACI = BCI
=> IBC + ICB = B+C/2
=> IBC + ICB = \(\frac{110°}{2}\)= 55°
Xét ∆BIC ta có :
BIC + IBC + ICB = 180°
=> IBC = 180° - 55°
=> IBC = 125°
Ta có :
Góc ngoài tại B = 180° - ABC
Góc ngoài tại C = 180° - ACB
Mà ABC + ACB = 110°
=> Góc ngoài B + góc ngoài C = 70°
Vì BK là phân giác góc ngoài B
CK là phân giác góc ngoài C
=> CBK + BCK = \(\frac{70°}{2}=35°\)
Xét ∆KCB ta có :
BKC + CBK + BCK = 180°
=> BKC = 180° - 35° = 145°
23 tháng 7 2019
Vì BI và CI là phân giác ABC và ACB
=> ABI = IBC
=> ACI = ICB
=> BIC = 180° - ( IBC + ICB )
Mà ABC + ACB = 180° - A
=> IBC + ICB = \(\frac{180°-\alpha}{2}\)
=> BIC = 180° - \(\frac{180°-\alpha}{2}\)
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
13 tháng 11 2023
Xét tg ABC có
\(\widehat{B}+\widehat{C}=180^o-\widehat{A}=180^o-68^o=112^o\)
\(\widehat{KBC}=\dfrac{\widehat{ABx}-\widehat{B}}{2}=\dfrac{180^o-\widehat{B}}{2}=90^o-\dfrac{\widehat{B}}{2}\)
\(\widehat{KCB}=\dfrac{\widehat{ACy}-\widehat{C}}{2}=\dfrac{180^o-\widehat{C}}{2}=90^o-\dfrac{\widehat{C}}{2}\)
Xét tg KBC có
\(\widehat{BKC}=180^o-\left(\widehat{KBC}+\widehat{KCB}\right)=\)
\(=180^o-\left(90^o-\dfrac{\widehat{B}}{2}+90^o-\dfrac{\widehat{C}}{2}\right)=\dfrac{\widehat{B}+\widehat{C}}{2}=\dfrac{112^o}{2}=56^o\)