Tìm x: (x-1)(x-4)(x-5)(x-8)+36=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 6 2019
\(2x+\left(1+2+3+...+100\right)=15150\)
\(2x+\left[\left(1+100\right)+\left(2+99\right)+...+\left(50+51\right)\right]=15150\)
\(2x+\left[101+101+...+101\right]=15150\)CÓ 50 SỐ 101
\(2x+\left[101\times50\right]=15150\)
\(2x=15150:5050\)
\(2x=3\)
\(x=3:2\)
\(x=1.5\)
SS
22 tháng 6 2019
a, 2x + (1+2+3+4+...+100) = 15150
=> 2x + \(\frac{\left(1+100\right).\left[\left(100-1\right)+1\right]}{2}\)= 15150
=> 2x + \(\frac{101.100}{2}\)= 15150
=> 2x + 5050 = 15150
=> 2x = 15150 - 5050
=> 2x = 10100
=> x = 10100 : 2
=> x = 5050
Vậy x = 5050
b, .(x+1)+(x+2)+(x+3)+(x+4)+(x+5)+(x+6)+(x+7)+(x+8)=36
=> (x + x + x + x +x + x +x +x ) + (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8) = 36
=> 8x + 36 = 36
=> 8x = 0
=> x = 0
Vậy x = 0
c, 0+0+4+6+8+...+2x=110
Sửa đề :0 + 2 + 4 + 6 + 8 + ... + 2x = 110 = 2 + 4 + 6 + 8 + ... + 2x = 110
SSH : \(\frac{\left(2\text{x}-2\right)}{2}+1=x-1+1=x\)
Tổng : \(\frac{\left(2\text{x}+2\right).x}{2}=110\Leftrightarrow\frac{2.\left(x+1\right).x}{2}=110\)
\(\Leftrightarrow\left(x+1\right)x=110\)
\(\Leftrightarrow\left(10+1\right).10=110\)
=> x = 10
Vậy x = 10
6 tháng 12 2018
\(\left(x-1\right)\left(x-4\right)\left(x-5\right)\left(x-8\right)+36=0\)
\(\Rightarrow\left(x-1\right)\left(x-8\right)\left(x-4\right)\left(x-5\right)+36=0\)
\(\Leftrightarrow\left(x^2-8x-x+8\right)\left(x^2-4x-5x+20\right)+36=0\)
\(\Rightarrow\left(x^2-9x+8\right)\left(x^2-9x+20\right)+36=0\)
\(\Rightarrow\left(x^2-9x+14-6\right)\left(x^2-9x+14+6\right)+36=0\)
\(\Rightarrow\left(x^2-9x+14\right)^2-36+36=0\)
\(\Rightarrow x^2-9x+14=0\Leftrightarrow\left(x-2\right)\left(x-7\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=7\end{matrix}\right.\)
Bài 1.
6 tháng 2 2021
a) \(15-5\left|x+4\right|=-12-3\)
\(\Leftrightarrow5\left|x+4\right|=30\)
\(\Leftrightarrow\left|x+4\right|=6\)
\(\Leftrightarrow\orbr{\begin{cases}x+4=6\\x+4=-6\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=2\\x=-10\end{cases}}\)
b) \(\left(4x-8\right)\left(7-x\right)=0\Leftrightarrow\orbr{\begin{cases}4x-8=0\\7-x=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=2\\x=7\end{cases}}\)
c) \(\left(x^2-36\right)\left(x^2+5\right)=0\Rightarrow\left(x-6\right)\left(x+6\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-6=0\\x+6=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=6\\x=-6\end{cases}}\)
d) \(-3\left(x+7\right)-11=2\left(x+5\right)\)
\(\Leftrightarrow-3x-32=2x+10\)
\(\Leftrightarrow5x=-42\Rightarrow x=-\frac{42}{5}\)
10 tháng 12 2021
\(a,\Leftrightarrow2x^2+10x-2x^2=12\Leftrightarrow x=\dfrac{12}{10}=\dfrac{6}{5}\\ b,\Leftrightarrow\left(5-2x-4\right)\left(5-2x+4\right)=0\\ \Leftrightarrow\left(1-2x\right)\left(9-2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{9}{2}\end{matrix}\right.\\ c,\Leftrightarrow3x^2-3x^2+6x=36\Leftrightarrow x=6\\ d,\Leftrightarrow2\left(x+5\right)-x\left(x+5\right)=0\\ \Leftrightarrow\left(2-x\right)\left(x+5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\\ e,\Leftrightarrow4x^2-4x+1-4x^2+196=0\\ \Leftrightarrow-4x=-197\Leftrightarrow x=\dfrac{197}{4}\)
\(f,\Leftrightarrow x^2+8x+16-x^2+1=16\Leftrightarrow8x=-1\Leftrightarrow x=-\dfrac{1}{8}\\ g,Sửa:\left(3x+1\right)^2-\left(x+1\right)^2=0\\ \Leftrightarrow\left(3x+1-x-1\right)\left(3x+1+x+1\right)=0\\ \Leftrightarrow2x\left(4x+2\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\end{matrix}\right.\\ h,\Leftrightarrow x^2+8x-x-8=0\\ \Leftrightarrow\left(x+8\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-8\end{matrix}\right.\\ i,\Leftrightarrow2x^2-13x+15=0\\ \Leftrightarrow2x^2+2x-15x-15=0\\ \Leftrightarrow\left(x+1\right)\left(2x-15\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=\dfrac{15}{2}\end{matrix}\right.\)
13 tháng 1 2020
1) x - 36 + 12 = - x+ 10
=> x + x = 10 + 24
=> 2x = 34
=> x = 34/2 = 17
2) (x + 15) - (11 - x) = (-2)2
=> x + 15 - 11 + x = 4
=> 2x = 4 - 4
=> 2x = 0
=> x = 0
3) 40 - 4x2 = (-6)2
=> 40 - 4x2 = 36
=> 4x2 = 40 - 36
=> 4x2 = 4
=> x2 = 1
=> x = \(\pm\)1
4) (-50) + 10x2 = (-25) x |-2|
=> -50 + 10x2 = -50
=> 10x2 = -50 + 50
=> 10x2 = 0
=> x2 = 0
=> x = 0
5) |x + 1| = 2020
=> \(\orbr{\begin{cases}x+1=2020\\x+1=-2020\end{cases}}\)
=> \(\orbr{\begin{cases}x=2019\\x=-2021\end{cases}}\)
6) (x + 1)5 + 8 = 0 (xem lại đề)
7) (-20) + x3 : 16 = -24
=> x3 : 16 = -24 + 20
=> x3 : 16 = -4
=> x3 = -4 . 16
=> x3 = -64 = (-4)3
=> x = -4
9) x14 = x17
=> x14 - x17 = 0
=> x14(1 - x3) = 0
=> \(\orbr{\begin{cases}x^{14}=0\\1-x^3=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=0\\x=1\end{cases}}\)
10) (-36) + (1 - x)2 = 0
=> (1 - x)2 = 36
=> (1 - x)2 = 62
=> \(\orbr{\begin{cases}1-x=6\\1-x=-6\end{cases}}\)
=> \(\orbr{\begin{cases}x=-5\\x=7\end{cases}}\)
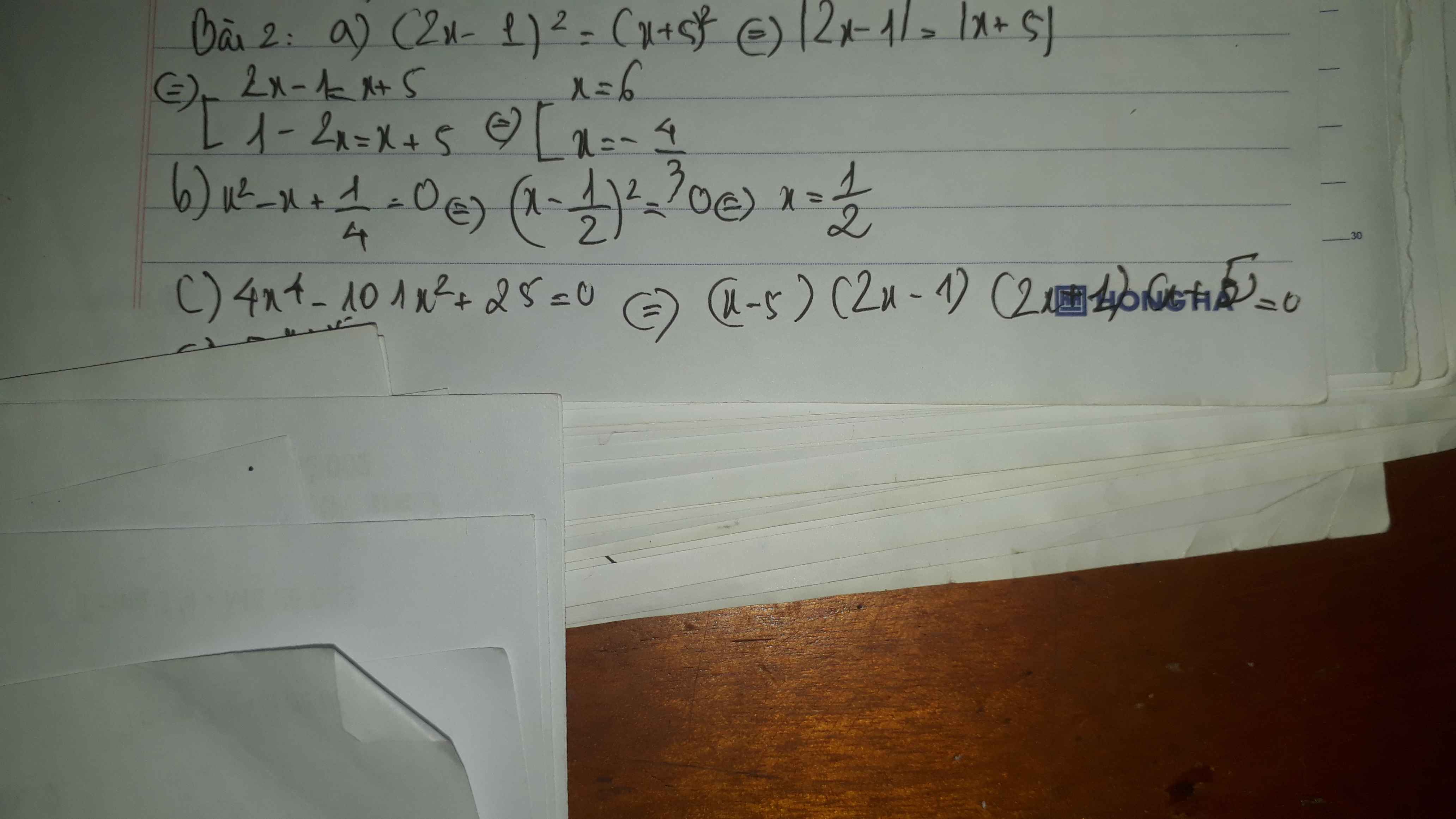
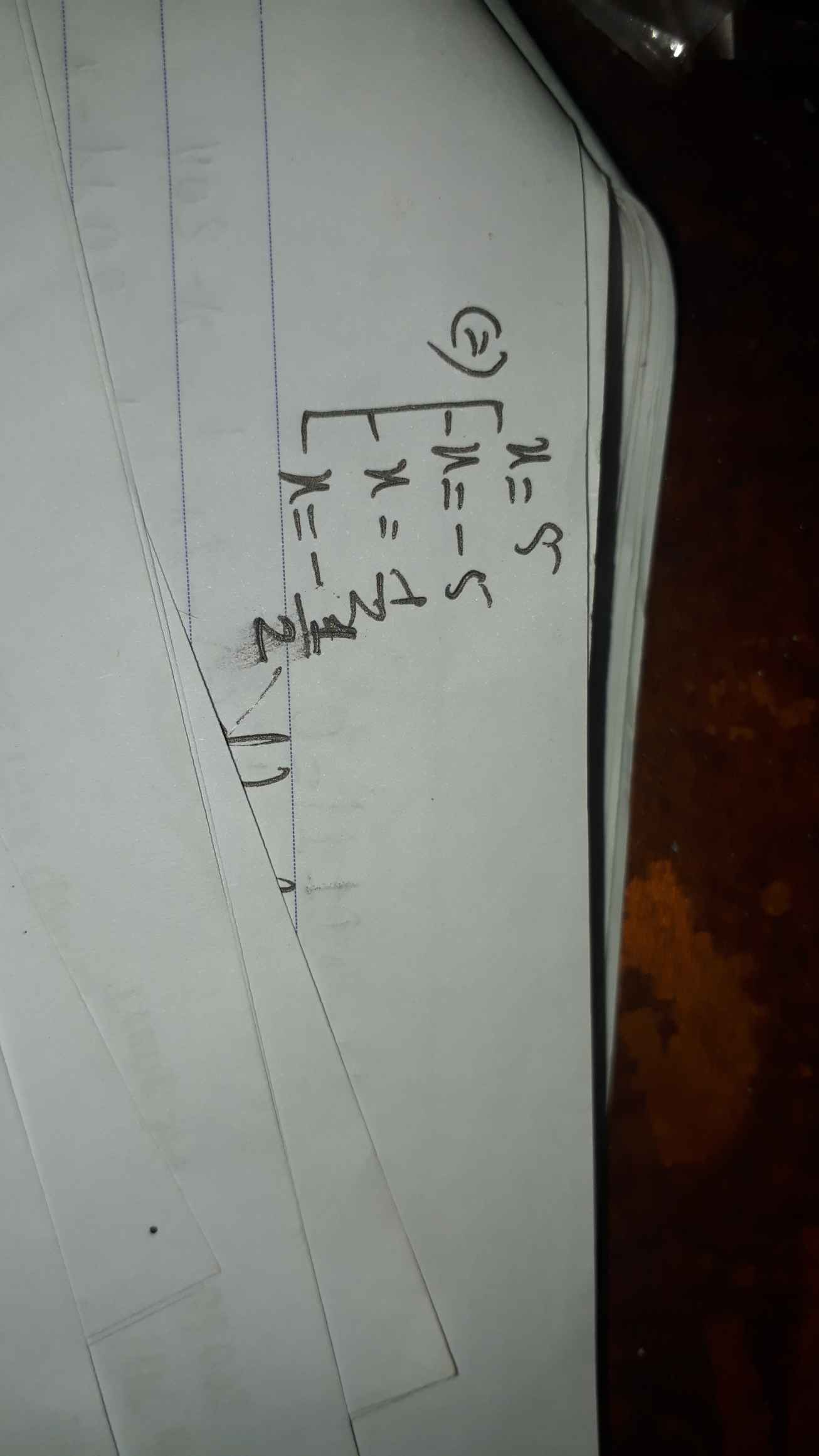
(-5)+(-11)
\(\left(x-1\right)\left(x-4\right)\left(x-5\right)\left(x-8\right)+36=0\)
\(\left[\left(x-1\right)\left(x-8\right)\right]\left[\left(x-4\right)\left(x-5\right)\right]+36=0\)
\(\left(x^2-9x+8\right)\left(x^2-9x+20\right)+36=0\)
Đặt \(a=x^2-9x+14\)ta có :
\(\left(a-6\right)\left(a+6\right)+36=0\)
\(a^2-6^2+36=0\)
\(a^2=0\)
Thay \(a=x^2-9x+14\)ta có :
\(\left(x^2-9x+14\right)^2=0\)
\(\Leftrightarrow x^2-9x+14=0\)
\(\Leftrightarrow x^2-2x-7x+14=0\)
\(\Leftrightarrow x\left(x-2\right)-7\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-7\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x-2=0\\x-7=0\end{cases}\Rightarrow\orbr{\begin{cases}x=2\\x=7\end{cases}}}\)
Vậy,...........